Статистика - дизайн информации - Элементы комбинаторики, статистики и теории вероятностей

Цель: рассмотреть статистическую обработку информации и ее основные характеристики.

Ход уроков

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

1. Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить из цифр 0, 3, 4, 8?

2. Из 24 участников собрания надо выбрать председателя, его заместителя и секретаря. Сколькими способами эго можно сделать?

3. Миша имеет восемь, а Витя - семь различных конфет. Сколькими способами мальчики могут поменяться пятью конфетами?

Вариант 2

1. Сколько различных трехзначных чисел, в которых цифры не повторяются, можно составить из цифр 0, 4, 5?

2. Из 28 спортсменов надо выбрать капитана команды и его заместителя. Сколькими способами это можно сделать?

3. Коля имеет девять, а Леша - восемь различных конфет. Сколькими способами мальчики могут поменяться шестью конфетами?

III. Изучение нового материала

Наш XXI в. характеризуют различным образом: век генной инженерии, век новых технологий (в частности, нанотехнологий), век астрофизики (проверка основополагающих космогонических теорий, большой андронный коллайдер) и т. д. Если вдуматься, все определения объединяет, прежде всего, получение принципиально новой информации. Поэтому правильнее назвать наш век веком информации. Буквально за несколько последних лет появились сверхмощные компьютеры, Интернет, различные поисковые системы, разрабатываются и совершенствуются методики обработки информации и т. п.

Многие из нас участвуют в переписи населения, выборах, опросах и т. д. При этом появляется определенная информация. Задача статистики - отражение этой информации и ее обработка. Для этого необходимо ввести некоторые статистические характеристики. Рассмотрим следующий пример.

Пример

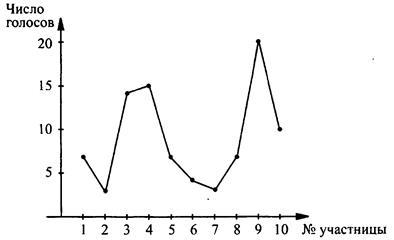
В финал конкурса “Мисс факультета” вышли 10 студенток, за которых болели и голосовали 90 студентов. В таблице приведены результаты голосования за участниц с номерами 1-10. Прежде всего возникает вопрос о наглядном отражении результатов голосования. Из алгебры вы знаете, что графическая информация нагляднее табличной. Поэтому применяют три вида графического отражения информации - диаграммы.

№ участницы	1	2	3	4	5	6	7	8	9	10
Число голосов	7	3	14	15	7	4	3	7	20	10

Первый вид диаграммы - линейная диаграмма (или многоугольник распределения) строится как обычный график. По оси абсцисс откладываются номера участниц, по оси ординат - число голосов, отданных за данную участницу, т. е. точки (1; 7), (2; 3); (3; 14) и т. д. Для наглядности отмеченные точки соединены отрезками.

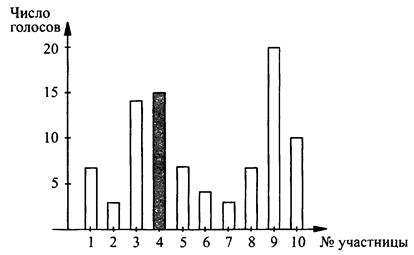
Второй вид диаграммы - столбчатая диаграмма (или гистограмма распределения) строится следующим образом. В окрестности каждой отмеченной точки по оси абсцисс строят прямоугольник, высота которого равна соответствующей ординате. При этом обычно ширину прямоугольников делают одинаковой. Достаточно часто прямоугольники изображаются таким образом, что два соседних имеют общую сторону. При этом прямоугольники могут штриховаться (см. учебник).

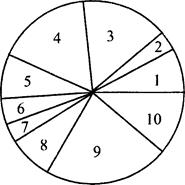
Третья диаграмма - круговая (или камамбер, по названию французского сыра) представляет собой круг, разделенный на 10 секторов с различными центральными углами. Так как всего было подано 90 голосов, то каждому голосу соответствует 360° : 90 = 4°. Далее легко пересчитать углы секторов. Например, для первой участницы строим сектор с углом 4° ∙ 7 = 28°. Каждый сектор маркируется номером соответствующей участницы.

На практике применяют все три вида диаграмм. Итак, на конкретном примере были рассмотрены основные этапы простейшей статистической обработки данных:

1. Систематизация, упорядочивание и группировка.

2. Составление таблицы распределения данных.

3. Построение диаграммы распределения данных (любого вида).

4. Паспорт данных измерения (основные характеристики информации).

Обсудим некоторые характеристики рассматриваемого примера.

Объем измерения - количество источников информации (т. е. число опрошенных или число голосов). В данном случае 90.

Размах измерения - разница между наибольшим и наименьшим значениями результатов измерения. В данном случае 20 - 3 = 17, так как наибольшее число поданных голосов 20, наименьшее - 3.

Мода измерения - наиболее часто встречающийся результат. В данном случае 9, так как за участницу № 9 было подано 20 голосов (наибольшее количество).

Среднее (или среднее арифметическое) - частное от деления суммы всех результатов измерения на объем измерения. Обычно его вычисляют после составления таблицы распределения. В данном случае получают:

Обычно результатами измерений являются некоторые числа. Каждое число, встретившееся в конкретном измерении, называют вариантой измерения. В конкретном измерении его варианты могут быть никак не связаны (например, билетики с результатами голосования). Однако обычно результаты обрабатываются. Если записать все варианты измерения в некотором порядке (например, по времени поступления голосов в жюри), то получится ряд данных измерения. Обычно упорядочивание происходит определенным образом. Запишем полученные варианты в порядке их возрастания (точнее, неубывания). Получим сгруппированный ряд данных:

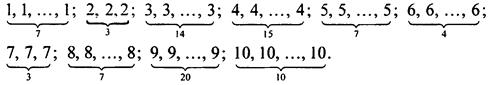
Среднюю варианту в сгруппированном ряде данных в случае нечетного количества чисел или среднее арифметическое двух стоящих посередине вариант в случае четного количества чисел называют медианой измерения. В нашем случае средних варианты две, это варианты 45 и 46. Каждая из них равна 5, значит, и медиана равна

В нашем примере ответ 1 встретился 7 раз (за участницу № 1 проголосовали 7 человек). Поэтому говорят, что абсолютная частота (или кратность) варианты 1 равна семи. Поэтому (в другой терминологии) ранее приведенная таблица имеет вид:

Варианта	1	2	3	4	5	6	7	8	9	10	Сумма
Кратность	7	3	14	15	7	4	3	7	20	10	90

Таким образом, получаем таблицу распределения данных измерения. Графа “Сумма” добавляется для контроля: число в этой графе обязательно равняется объему измерения.

Заметим, что при вычислении среднего арифметического в неявном виде уже использовалось понятие кратности варианты.

Введем еще понятие частоты данной варианты - частное от деления кратности варианты на объем измерения. Например, для варианты 1 находим частоту Частоту варианты можно выразить в процентах. Тогда получим:

IV. Контрольные вопросы

1. Основные задачи статистики.

2. Виды диаграмм распределения и их построение.

3. Объем измерения.

4. Понятие размаха измерения.

5. Мода измерения.

6. Среднее арифметическое.

7. Понятие медианы измерения.

8. Кратность и частота варианты.

V. Задание на уроках

§ 19, № 1,3, 5, 8, 10, 12, 17, 19.

VI. Задание на дом

§ 19, №2, 4, 6, 9, 11, 14, 18, 20.

VII. Подведение итогов уроков