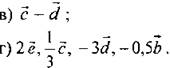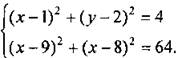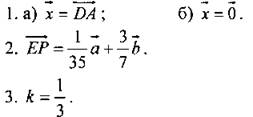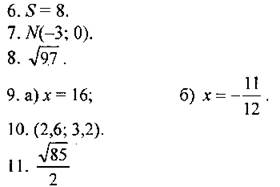Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
ИТОГОВОЕ ПОВТОРЕНИЕ ПО ТЕМЕ ВЕКТОРЫ. МЕТОД КООРДИНАТ. ДВИЖЕНИЯ - НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ СТЕРЕОМЕТРИИ
|
Цель деятельности учителя |
Создать условия для систематизации знаний по теме “Векторы. Метод координат. Движение”, повторения основных определений, свойств, признаков; для подготовки к сдаче ГИА |
|
|
Термины и понятия |
Вектор, длина вектора, сложение векторов и его свойства, умножение вектора на число и его свойства, коллинеарные векторы, прямоугольные координаты точек на плоскости, формула расстояния между двумя точками плоскости с заданными координатами, координаты середины отрезка, уравнения окружности и прямой, применение векторов и метода координат к доказательству теорем и решению задач; движения |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют работать с геометрическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, осуществлять классификации, проводить логические обоснования, доказательства математических рассуждений |
Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач; владеют логическими действиями определения понятий, обобщения, установления аналогий. Регулятивные: принимают и сохраняют цели и задачи учебной деятельности. Коммуникативные: умеют формулировать, аргументировать и отстаивать свое мнение, работать в группе. Личностные: проявляют ответственное отношение к учению, готовность и способности к саморазвитию и самообразованию на основе мотивации к обучению и познанию |
|
|
Организация пространства |
||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|
|
Образовательные ресурсы |
• Задания для индивидуальной работы, самостоятельной работы, домашней работы |
|
|
I этап. Актуализация опорных знаний учащихся |
||
|
Цель деятельности |
Совместная деятельность |
|
|
Систематизировать теоретические знания учащихся по данной теме |
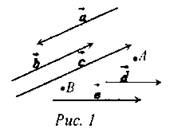
1. Ответить на вопросы учащихся по домашнему заданию. 2. Дано:
Укажите: а) коллинеарные векторы; б) сонаправленные векторы; в) противоположно направленные векторы; г) равные векторы; д) нулевые векторы. Найдите: длины векторов Постройте: а) сумму векторов б) сумму векторов
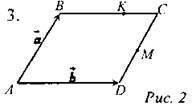
Дано: ABCD - параллелограмм, К є ВС, ВК : КС = 2 : 1, М - середина CD. Разложить векторы 4. Дано: А (3; -2), В(-5; 4), С (-1; -3). Найдите: а) координаты вектора б) длину вектора в) координаты середины отрезка АС; г) расстояние между точками A и В. 5. Дано: 6. Дано: 7. Дан треугольник АВС. Постройте его образ: а) при осевой симметрии относительно прямой АВ; б) при центральной симметрии относительно точки С; в) при параллельном переносе на вектор г) при повороте вокруг точки А на угол 45° по часовой стрелке |
|
|
II этап. Самостоятельная работа |
||
|
Цель деятельности |
Задания для самостоятельной работы |
|
|
Совершенствовать навыки решения задач |
(И) 1. ABCD и ADEF - параллелограммы, имеющие общую сторону. Постройте вектор
2. На стороне CD и диагонали АС параллелограмма ABCD лежат точки Р Е так, что DP : PC = 3 : 2, АЕ : ЕС = 4 : 3. Выразите вектор 3. В треугольнике MNK О - точка пересечения медиан, 4. На окружности с центром О постройте такие точки, что:
5. Докажите, что если для четырехугольника ABCD и произвольной точки О выполняется равенство 6. Докажите, что четырехугольник MNKP, заданный координатами своих вершин М(2; 2), N(5; 3), К(6; 6), P(3; 5), является ромбом, и вычислите его площадь. 7. Найдите координаты точки N, лежащей на оси абсцисс и равноудаленной от точек Р(-1; 3) и K(0; 2). 8. В равнобедренном треугольнике основание равно 12 см, а высота, проведенная к основанию, равна 8 см. Найдите медиану, проведенную к боковой стороне. 9. Определите значение х, при котором вектор 10. Используя метод координат, решите систему уравнений 11. В четырехугольнике ABCD АВ = AD = 5, ВС = CD = 3√2, АС = 7. Используя метод координат, найдите расстояние между серединами противолежащих сторон четырехугольника. Ответы к тестовым задачам.
4. а) АВ - диаметр; б)
|
|
|
III этап. Итоги урока. Рефлексия |
||
|
Деятельность учителя |
Деятельность учащихся |
|
|
(Ф/И) - Какие темы повторили на уроке? - Задайте три вопроса по уроку |
(И) Домашнее задание: подготовиться к итоговой контрольной работе. Решить задачи: 1. Дан правильный шестиугольник ABCDEF со стороной а. Найдите скалярное произведение векторов: 2. Найдите косинусы углов треугольника АВС, если А(1; 3), В(8; 2), С(5; -1). 3. В параллелограмме ABCD диагональ BD равна стороне ВС, точка М - середина стороны ВС, отрезок DMперпендикулярен к диагонали АС. Найдите углы параллелограмма. 4. Две окружности радиуса г с центрами O1 и O2 касаются друг друга в точке М. На первой окружности отмечена точка А, а на второй - точка В так, что хорды AM и ВМ взаимно перпендикулярны. Докажите, что: 1) при параллельном переносе на вектор |
|