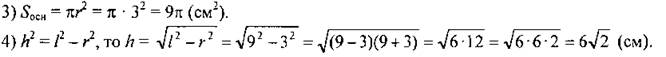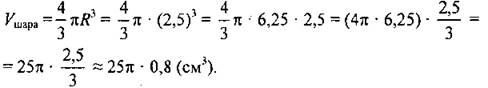Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
СФЕРА И ШАР - НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ СТЕРЕОМЕТРИИ
|
Цели деятельности учителя |
Создать условия для введения понятий “сфера”, “центр сферы”, “радиус сферы”, “диаметр”, определения шара, для обучения изображению шара; рассмотрения доказательств теоремы об объеме шара и площади сферы; способствовать развитию умения решать задачи |
||
|
Термины и понятия |
Шар, сфера, радиус |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют объяснять, какое тело называется шаром, что такое сфера |
Познавательные: умеют создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач; осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий. Регулятивные: принимают и сохраняют цели и задачи учебной деятельности. Коммуникативные: умеют формулировать, аргументировать и отстаивать свое мнение. Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||
|
Образовательные ресурсы |
• Задания для проверочной работы |
||
|
I этап. Актуализация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Выявить трудности, возникшие при выполнении домашнего задания |
(Ф/И) 1. Обсуждение вопросов учащихся по домашнему заданию. 2. Проверка решения № 1249 и 1250 на доске. № 1249. По условию h = 12 см, V = 324π см3. Найти α-дугу развертки боковой поверхности конуса.
Ответ: α = 216°. № 1250. По условию α = 120°. Радиус развертки боковой поверхности конуса равен образующей конуса, то есть l = r1 = 9 см, где r1 - радиус сектора.
2) С другой стороны, Sбок = πrl, значит, 27π = π ∙ r ∙ 9, отсюда r = 3 см (это радиус конуса).
Ответ: 9π см2; 6√2 см. 3. Проверочная работа (10 мин). Учащиеся на отдельных листках отвечают на вопросы, выполняют построения, а затем сдают работы на проверку учителю. Вариант I 1. Объясните, какое тело называется цилиндром; что такое ось, высота, основание, радиус, боковая поверхность, образующие цилиндра. Выполните построение цилиндра. 2. Какой формулой выражается объем цилиндра? Запишите формулу. 3. Объясните, как получается и что представляет собой развертка боковой поверхности цилиндра. 4. Запишите формулу площади боковой поверхности цилиндра. Вариант II 1. Объясните, какое тело называется конусом; что такое ось, высота, основание, боковая поверхность, образующие конуса. Выполните построение конуса. 2. Какой формулой выражается объем конуса? Запишите формулу. 3. Объясните, как получается и что представляет собой развертка боковой поверхности конуса. 4. Запишите формулу площади боковой поверхности конуса |
||
|
II этап. Изучение новой темы |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Ввести понятия сферы и шара |
(И) 1. Учащиеся самостоятельно изучают материал пункта 131 “Сфера и шар” (с. 322-323). Затем учитель показывает на доске изображения сферы и шара (рис. 364, 365), а учащиеся выполняют построение сферы и шара в тетрадях. 2. В тетрадях учащиеся записывают: а) Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. Данная точка называется центром сферы, а данное расстояние - радиусом сферы. б) Отрезок, соединяющий две точки сферы и проходящий через ее центр, называется диаметром сферы. в) Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара. г) Объем шара радиуса R равен д) Плошадь сферы радиуса R равна 4πR2.
|
||
|
III этап. Решение задач |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
Совершенствовать навыки решения задач на изученную тему |
(Ф/И) Организует деятельность учащихся. 1. Решить задачу № 1226 (б, в) (самостоятельно). 2. Решить задачу № 1227 на доске и в тетрадях. 3. Решить задачу № 1229 (самостоятельно, затем решение задачи проверяется). 4. Решить задачу № 1228 практического содержания. 5. Решить задачу № 1231 на доске и в тетрадях |
№ 1227. Диаметр Луны составляет (приближенно) четвертую часть диаметра Земли, то есть dЗемли= 4dЛуны, тогда радиус Земли в 4 раза больше радиуса Луны, то есть R1 = 4R2. Найдем объем Луны Найдем объем Земли
Значит, объем Земли в 64 раза больше объема Луны. Ответ: в 64 раза. № 1229. По условию R = 10 см. По формуле S = 4πR2 найдем площадь сферы (покрышки футбольного мяча).
8 % = 0,08 от 1256 равно 1256 ∙ 0,08 = 100,48 (см2). На покрышку футбольного мяча необходимо кожи: 1256 + 100,48 = 1356,48 ≈ 1357. Ответ: ≈ 1357 см2. № 1228.
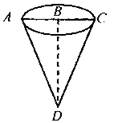
По условию BD = h = 12 см; АС = 5 см, тогда ВС = r = 2,5 см. Найдем объем конуса (объем стаканчика для мороженого):
Положим две ложки мороженого в виде полушарий, тогда вместе они составляют шар диаметром 5 см, то есть радиусом 2,5 сантиметра. Найдем объем шара (объем мороженого):
Значение выражения 25π ∙ 0,8 меньше значения выражения 25π. Поэтому объем шара (объем мороженого) меньше объема конуса (объема стаканчика для мороженого). Значит, мороженое, если оно растает, не переполнит стаканчик. Ответ: нет. № 1231. Отношение объемов двух шаров равно кубу коэффициента подобия, так как любые шары - это подобные тела.
По условию Аналогично теореме “Отношение площадей двух подобных треугольников (фигур) равно квадрату коэффициента подобия” (см. пункт 58 на с. 139 учебника) имеем, что отношение площадей поверхностей двух подобных тел равно квадрату коэффициента подобия.
Так как k = 2, то Ответ: 4:1. |
|
|
IV этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) - Какое тело изучили на уроке? - Чем отличается шар от сферы? - Задайте три вопроса по теме урока |
(И) Домашнее задание: изучить материал пункта 131, ответить на вопросы 23-26, записать в тетради решения задач 1224, 1225 |
||
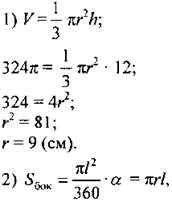 отсюда, сократив обе части равенства на πl, получим
отсюда, сократив обе части равенства на πl, получим