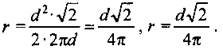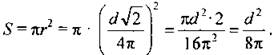Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
ЦИЛИНДР - НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ СТЕРЕОМЕТРИИ
|
Цель деятельности учителя |
Создать условия для введения понятий цилиндра, цилиндрической поверхности, образующих цилиндр, для доказательства теорем об объеме цилиндра, о площади боковой поверхности цилиндра, для обучения применению этих теорем при решении задач |
|||
|
Термины и понятия |
Ось цилиндра, его высота, основания цилиндра, образующая, боковая поверхность |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Умеют объяснять какое тело называется цилиндром, что такое его ось, высота, основания, боковая поверхность, образующая, развертка |
Познавательные: умеют видеть математическую задачу в контексте проблемной ситуации, устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и формулировать выводы. Регулятивные: принимают и сохраняют цели и задачи учебной деятельности. Коммуникативные: умеют формулировать, аргументировать и отстаивать свое мнение. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные ресурсы |
• Задания для построения |
|||
|
I этап. Актуализация опорных знаний учащихся |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Систематизировать знания учащихся по изученным темам |
(Ф) 1. Обсуждение вопросов учащихся по домашнему заданию. 2. Практическая работа. 1) Построить правильную треугольную пирамиду, четырехугольную пирамиду, шестиугольную пирамиду. 2) Провести высоты и апофемы. 3) Найти объемы этих пирамид, если высота равна 1, сторона основания равна 1. Ответы: треугольная: |
|||
|
II этап. Учебно-познавательная деятельность |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Ввести понятие цилиндра и его элементов |
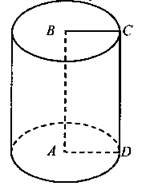
(Ф) 1. Ознакомить учащихся с цилиндром. - Возьмем прямоугольник ABCD и будем вращать его вокруг одной из сторон, например, вокруг стороны АВ (рис. 360). В результате получится тело, которое называется цилиндром. Учитель показывает модель цилиндра.
2. Организовать построение на доске и в тетрадях изображения цилиндра и его частей (рис. 360 на с. 319). - Прямая АВ называется осью цилиндра, а отрезок АВ - его высотой. При вращении сторон AD и ВС образуются два равных круга - они называются основаниямицилиндра, а их радиус называется радиусом цилиндра. При вращении стороны CD образуется поверхность, состоящая из отрезков, параллельных оси цилиндра. Ее называют цилиндрической поверхностью или боковой поверхностью цилиндра, а отрезки, из которых она составлена, - образующими цилиндра. Таким образом, цилиндр - это тело, ограниченное двумя равными кругами и цилиндрической поверхностью. 3. Рассмотреть решение задачи № 1213 (рис. 366, с. 326). Пользуясь принципом Кавальери, можно доказать, что объем цилиндра равен произведению площади основания на высоту.
где S - площадь основания; h - высота цилиндра. 4. Ввести понятие развертки боковой поверхности цилиндра, используя рисунок учебника (рис. 361). Записать в тетрадях: “Площадь боковой поверхности цилиндра равна площади ее развертки, то есть |
|||
|
III этап. Закрепление изученного материала |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
На простейших задачах отработать основные понятии цилиндра |
(Ф/И) Организует деятельность учащихся. 1. Решить задачу № 1214 (б; в) на доске и в тетрадях. 2. Решить задачу № 1216. (Учащиесярешают задачу самостоятельно, а затем проверяется решение.) 3. Решить задачу № 1217. Задача практического характера. 4. Решить задачу № 1245. 5. Решить задачу № 1246. (Учитель объясняет решение.) 6. Решить задачу № 1247 |
№ 1214. б) Дано: V = 120 см3; h = 3,6 см. Найти: r. Решение: V = Sh, отсюда Ответ: в) Дано: r = h; V = 8π см3. Найти: h. Решение:
Ответ: 2. № 1216. Дано: диаметр d = 1 м; h = с (длина окружности основания). Найти: Sбок. Решение: Длина окружности равна с = 2πr = πd; по условию h = с, тогда h = πd = π ∙ 1 м = π (м).
Ответ: π2 м2. № 1217. Дано: h = 4 м; d = 20 см. Найти: Sбок. Решение:
Найдем 2,5 % от 0,8π2. 2,5 % = 0,025; тогда 0,8π ∙ 0,025 = 0,02π (м2). Всего пойдет жести:
Ответ: ≈ 2,58 м2. № 1245. Решение: Плотность свинца ρ = 11,4 г/см3; h = 25 м = 2500 см.
Основание свинцовой трубы представляет собой кольцо. Найдем площадь кольца по формуле
Объем свинцовой трубы равен:
Ответ: 61 кг. № 1246. Дано: по условию задачи h > r на 12 см, тогда h = r + 12 см. Sполной поверхности = 288π см2. Найти: r и h. Решение:
По условию Sполн. = 288π (см2), тогда 4πr2 + 24πr = 288π; разделим обе части равенства на 4π, получим: r2 = 6r - 72 = 0. r1 = 6; r2 = -12 - не удовлетворяет условию задачи. Значит, радиус цилиндра равен 6 см, а высота цилиндра 6 + 12 = 18 (см). Ответ: 6 см; 18 см. № 1247. Решение:
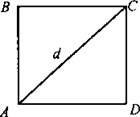
Обозначим сторону квадрата х, тогда из ∆ADC по теореме Пифагора найдем d2 = х2 + х2 = 2x2;
Мы знаем, что Площадь основания цилиндра равна
Ответ: d2/8π |
||
|
IV этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) - С каким цветом радуги ассоциируется данный урок? • Оранжевый - радостное, восторженное настроение; • красный - нервозное, возбужденное состоянии, агрессия; • синий цвет - грустное настроение, пассивность, усталость, желание отдохнуть; • зеленый цвет - активность; • желтый цвет - цвет радости; • фиолетовый цвет - беспокойное, тревожное настроение, близкое к разочарованию |
(И) Домашнее задание: изучить материал пункта 129, решить задачи № 1214 (а) и № 1244 |
|||
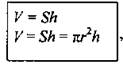
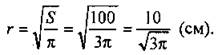
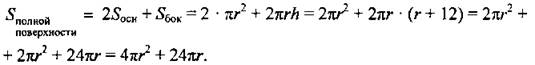
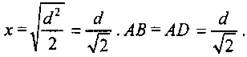
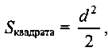 значит,
значит,