ПРИЗМА. ПАРАЛЛЕЛЕПИПЕД - НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ СТЕРЕОМЕТРИИ

Цель деятельности учителя

Создать условия для введения понятий призмы и ее элементов, прямой и наклонной призмы, высоты призмы, параллелепипеда, прямого и прямоугольного параллелепипеда, для обучения построению призмы и параллелепипеда

Термины и понятия

Призма, параллелепипед, грани, ребра

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют объяснять, что такое многогранник, его грани, ребра, вершины, диагонали, какой многогранник называется выпуклым, что такое я-угольная призма, ее основания, какая призма называется наклонной, параллеллепипедом

Познавательные: имеют первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и формулировать выводы.

Регулятивные: принимают и сохраняют цели и задачи учебной деятельности.

Коммуникативные: умеют формулировать, аргументировать и отстаивать свое мнение.

Личностные: проявляют креативность мышления, инициативность, находчивость, активность при решении геометрических задач

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные

ресурсы

• Задания для фронтальной и индивидуальной работы

I этап. Актуализация опорных знаний учащихся

Цель деятельности

Совместная деятельность

Систематизировать знания учащихся

(Ф) Устная работа:

- Какой раздел геометрии называется стереометрией?

- Что рассматривается в стереометрии?

- Какие поверхности называются многогранниками? Приведите примеры простейших многогранников.

- Какая плоскость называется секущей плоскостью геометрического тела?

- Что называется сечением тела?

- Объясните, что такое многогранник; грани, ребра, вершины и диагонали многогранника. Приведите примеры многогранников. (Учитель показывает модели различных геометрических тел и многогранников, а учащиеся должны назвать их.)

II этап. Изучение нового материала

Цель деятельности

Совместная деятельность

Ввести понятия призмы и параллелепипеда

(Ф)

1) Две плоскости называются параллельными, если они не имеют общих точек.

2) Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Определение.

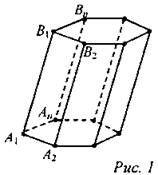
Призмой (n-угольной) называется многогранник, у которого две грани - равные n-угольники А₁А₂...А_n и В₁В₂...В_n (называемые основаниями) с соответственно параллельными сторонами, а остальные n граней - параллелограммы, у каждого из которых две стороны являются соответственными сторонами оснований.

Элементы призмы

Название

Определение

Обозначения на чертеже

Чертеж

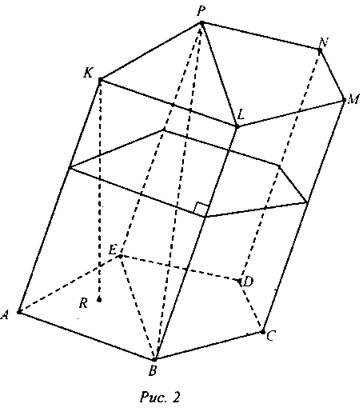
Основания

Две грани, являющиеся равными многоугольниками, лежащими в параллельных плоскостях

ABCDE, KLMNP

Боковые грани

Все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом

ABLK, ВСML, CDNM, DEPN, ЕАКР

Боковая поверхность

Сумма площадей боковых граней

S_бок = S₁ +...+ S_n

Полная поверхность

Сумма площадей двух оснований и боковой поверхности

S_пол = S_бок + 2S_осн

Боковые ребра

Общие стороны боковых граней. Боковые ребра призмы параллельны и равны

АК, BL, CM, DN, EP

Высота

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания

KR

Диагональ призмы

Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани

BP

Диагональная

плоскость

Плоскость, проходящая через боковое ребро призмы и диагональ основания

Диагональное

сечение

Пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе его частные случаи - ромб, прямоугольник, квадрат

EBLP

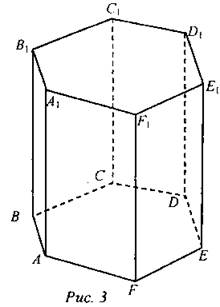
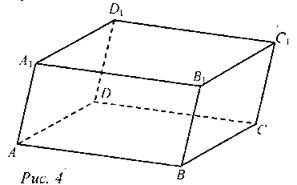
Прямая призма.

Определение. Призма называется прямой, если все ее боковые грани являются прямоугольниками.

Высота прямой призмы равна ее боковому ребру.

Правильная призма.

Определение. Призма называется правильной, если основаниями ее служат правильные многоугольники и боковые ребра перпендикулярны к основаниям.

В зависимости от числа углов в основании призма называется треугольной, четырехугольной, пятиугольной и т. д.

Боковыми гранями любой правильной призмы служат прямоугольники.

Параллелепипед.

Определение. Параллелепипед - призма, основаниями которой являются параллелограммы.

Типы параллелепипеда:

Прямоугольный параллелепипед - это параллелепипед, у которого все грани - прямоугольники. Прямой параллелепипед - это параллелепипед, у которого 4 боковые грани - прямоугольники.

Куб - это прямоугольный параллелепипед с равными измерениями. Все шесть граней куба - равные квадраты.

Основные элементы параллелепипеда:

Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро - смежными. Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параплелепипеда. Длины трех ребер прямоугольного параллелепипеда,

имеющих общий конец, называют его измерениями.

Свойства:

• Параллелепипед симметричен относительно середины его диагонали.

• Любой отрезок с концами, принадлежащими поверхности параллелепипеда, проходящий через середину его диагонали, делится ею пополам; в частности,

все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.

• Противолежащие грани параллелепипеда параллельны и равны.

• Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений

III этап. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

Научить решать простейшие задачи по теме

(Ф/И)

1. Решить задачу № 1185.

2. Решить задачу № 1186.

3. Решить устно № 1187, используя модель параллелепипеда.

Ответ: а) нет; б) нет; в) нет; г) да; д) нет.

№ 1185.

а) Число вершин призмы определяется количеством вершин многоугольника, лежащего в основаниях призмы. Так как призма имеет два основания, то n-угольная призма имеет 2n вершин (четное число). Например: треугольная призма имеет 2 ∙ 3 = 6 вершин; четырехугольная призма имеет 2 ∙ 4 = 8 вершин; пятиугольная призма имеет вершин 5 ∙ 2 = 10.

б) Число ребер призмы равно сумме ребер двух оснований призмы и боковых ребер призмы, количество которых определяется числом вершин многоугольника, расположенного в основании призмы, то есть n-угольная призма имеет число ребер, равное 2n + n = 3n кратно 3.

№ 1186.

Площадь боковой поверхности прямой призмы равна сумме площадей ее боковых граней. Пусть а, b, с, d... m - стороны основания призмы; h - ее боковое ребро.

У прямой призмы все боковые ребра перпендикулярны к плоскостям оснований, то есть боковые грани - прямоугольники. Площадь прямоугольника равна произведению его смежных сторон. Тогда:

где P - периметр основания, h - боковое ребро.

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- С какими телами познакомились на уроке?

- Задайте три вопроса по теме урока.

- Составьте синквейн к уроку

(И) Домашнее задание: изучить материал пунктов 124 и 125; выполнить рисунки (рис. 346 а, б, в) и записать в тетрадях доказательство свойства диагоналей параллелепипеда; решить № 1190 (б) и № 1234 (б)