Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ В КООРДИНАТАХ. СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
|
Цель деятельности учителя |
Создать условия для доказательства теоремы о скалярном произведении двух векторов в координатах и ее следствий |
|||
|
Термины и понятия |
Косинус, угол между векторами, скалярное произведение, скалярный квадрат |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: понимают и используют математические средства наглядности для иллюстрации, интерпретации, аргументации; осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий. Регулятивные: понимают и сохраняют учебные задачи. Коммуникативные: участвуют в диалоге. Личностные: проявляют креативность мышления, инициативность, находчивость, активность при решении геометрических задач |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные ресурсы |
• Задания для проверочной работы |
|||
|
I этап. Актуализация опорных знаний учащихся |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Проверить уровень сформированности теоретических знаний |
(Ф/И) 1. Обсуждение вопросов учащихся по домашнему заданию. (И) 2. Проверочная работа на 10 минут. Вариант I 1. Известно, что 2. Дан вектор 3. Даны векторы 4. Найдите координаты вектора 5. Даны векторы 6. Две стороны треугольника равны 7 и 3 см, а угол между ними равен 120°. Найдите третью сторону треугольника. 7. В треугольнике АВС угол А = 45°, АВ = 2, АС = 3. Вычислите 8. Скалярное произведение ненулевых векторов Вариант II 1. Дан вектор 2. Известно, что 3. Найдите координаты вектора 4. Даны векторы 5. Даны векторы 6. В треугольнике MPQ угол ∠M = 135°, МР = 5, MQ = 2√2. Вычислите 7. Две стороны треугольника равны 3 и 9 м, а угол между ними равен 60°. Найдите третью сторону треугольника. 8. Чему равно скалярное произведение координатных векторов? |
|||
|
II этап. Изучение новой темы |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Доказать теорему, о скалярном произведении в координатах |
(Ф) 1. Теорема. В прямоугольной системе координат скалярное произведение векторов (Доказательство производится в диалоговом режиме.) 2. Следствия: 1) 2) Если 3. Свойства скалярного произведения векторов: а) Если 2) 3) 4) |
|||
|
III этап. Закрепление изученной темы |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
Совершенствовать навыки решения задач |
(Ф/И) 1. Решить на доске и в тетрадях № 1043 (с объяснением учителя). 2. Решить № 1044 (а, б). 3. Решить № 1045 (устно). 4. Решить задачи № 1046, 1047 (б, в) на доске и в тетрадях. 5. Решить задачу № 1051 |
№ 1043.
Дано: Найти: Решение:
|
||
|
IV этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) - Что нового узнали о скалярном произведении? - Задайте три вопроса по теме |
(И) Домашнее задание: изучить материал пунктов 107-108; ответить на вопросы 17-20 в учебнике на странице 267; решить № 1044 (в), 1047 (а), 1054 (разобрать решение задачи и записать в тетрадь); узнать, где применяется скалярное произведение |
|||
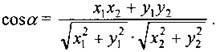
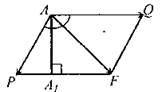
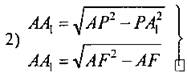 , следовательно,
, следовательно,