РЕШЕНИЕ ТРЕУГОЛЬНИКОВ. ИЗМЕРИТЕЛЬНЫЕ РАБОТЫ - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

Цель деятельности учителя

Создать условия для ознакомления учащихся с методами решения треугольников, закрепления знаний теорем синусов и косинусов, обучения применению теорем в ходе решения задач

Термины и понятия

Синус, косинус, треугольник, площадь треугольника, прилежащий угол, противолежащий угол, радиус окружности, описанный около треугольника

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют применить теоремы синусов и косинусов для решения треугольников

Познавательные: умеют понимать и использовать математические средства наглядности для иллюстрации, интерпретации, аргументации, видеть математическую задачу в контексте проблемной ситуации.

Регулятивные: принимают и сохраняют учебные задачи.

Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем, участвовать в диалоге.

Личностные: проявляют креативность мышления, инициативность, находчивость, активность при решении геометрических задач

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные

ресурсы

• Задания для фронтальной работы

I этап. Актуализация опорных знаний

Цель деятельности

Совместная деятельность

Проверить успешность учащихся в выполнении домашней работы

(Ф/И)

1. Сформулировать теорему о площади треугольника.

2. Сформулировать теорему синусов.

3. Сформулировать теорему косинусов.

4. Объяснить применение теоремы косинусов при решении треугольников.

5. Определить, в какой задаче на решение треугольников можно применять только теорему синусов.

6. Прочитать самостоятельно по учебнику решение № 1033 и записать решение в тетрадь.

7. Прочитать в учебнике п. 104 на с. 256-257

II этап. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

Совершенствовать навыки решения задач

(Ф/И) Решить задачи.

1) В треугольнике АВС ∠A = 20°, ∠В = 40°, АВ = 12 см. Найти радиус окружности, описанной около треугольника.

2) Стороны треугольника равны 12, 13 и 14. Найти радиус окружности, описанной около треугольника.

3) Решить № 1036, 1037, 1038 на доске и в тетрадях

Ответы:

1) R = 4√3.

2) R ≈ 7,55.

№ 1036.

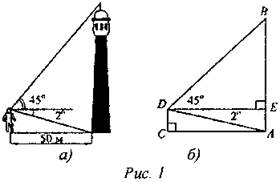
Воспользуемся рисунком 1б, который является схематичным изображением рисунка 1а, то есть рисунка на с. 298 учебника.

По условиям задачи АС = 50 м, ∠EDA = 2°, ∠EDB = 45°, ∠DEB = 90°. Требуется найти длину отрезка АВ.

Из треугольника ADE находим АЕ:

АЕ = DE ∙ tg2° = 50 ∙ tg2° ≈ 50 м ∙ 0,035 ≈ 2 м.

Треугольник DEB прямоугольный и равнобедренный, так как

∠DBE =180° - 90° - 45° = 45° = ∠BDE. Следовательно, BE = DE = AC = 50 м.

Таким образом, АВ = AE + BE ≈ 52 м.

Ответ: ≈ 52 м.

№ 1037.

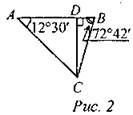
Дано: АВ = 70 м; ∠САВ = 12°30'; ∠АВС = 72°42'; CD ⊥ AB.

Найти: CD.

Решение:

1) В ∆AOC: CD = AD ∙ tg∠A, CD = AD ∙ tg12°30';

В ∆BDC: CD = BD ∙ tg∠5, CD = BD ∙ tg72°42';

2) Примем AD = x м, получим BD = 70 - x m.

x tg12°30’ = (70 - x) ∙ tg72°42';

x - 0,2217 = (70 - x) ∙ 3,21;

3,4327x = 224,77;

x ≈ 65,48.

AD = 65,48 m.

3) CD = 65,48 ∙ 0,2217 ≈ 14,52 m.

Ответ: 14,52 м.

№ 1038.

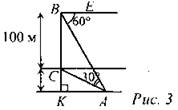
Дано: ∠ABE = 60°, ∠CAB = 30°, ВС = 100 м.

Найти: СК.

Решение:

1) Так как ∠CBE = 90°; ∠ABE = 60°, то ∠CBA = 30°, следовательно, ∆АВС - равнобедренный, ∠C = 120°, ВС = АС = 100 м.

2) Так как ∠BCA и ∠KCA - смежные, то ∠KCA = 60°, ∠KAC= 30°, СK = 1/2AC, СK = 50 м.

Ответ: 50 м

III этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Оцените свою деятельность на каждом этапе урока.

- Что для вас оказалось наиболее сложным?

(И) Домашнее задание: решить № 1034, 1060 (а), 1061 (а)