ТЕОРЕМА О ПЛОЩАДИ ТРЕУГОЛЬНИКА - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

Цель деятельности учителя

Создать условия для доказательства теоремы о площади треугольника

Термины и понятия

Синус, треугольник, площадь треугольника

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют применять определение синуса для доказательства теоремы

Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий.

Регулятивные: умеют видеть математическую задачу в контексте проблемной ситуации.

Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем.

Личностные: владеют коммуникативной компетентностью

Организация пространства

Формы работы

Фронтальная (Ф); парная (П); индивидуальная (И); групповая (Г)

Образовательные

ресурсы

• Задания для фронтальной, групповой работы

I этап. Актуализация опорных знаний

Цель деятельности

Совместная деятельность

Проверить выполнение домашнего задания

(Ф/И)

1. Проверить правильность выполнения домашнего задания, для этого пригласить к доске троих учащихся.

2. Вспомнить, какие формулы используются для вычисления площади треугольника и площади параллелограмма

II этап. Мотивация к деятельности

Цель деятельности

Деятельность учителя

Деятельность учащихся

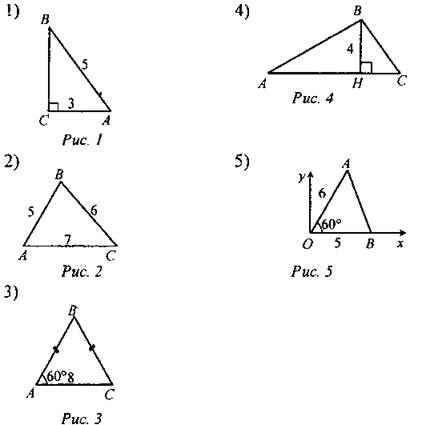
Совершенствовать навыки вычисления площади треугольника

(Ф) Вычислить площади треугольников:

Ответы:

1) 6.

2) 6√6.

3) 16√6.

4) 20.

5) 7,5√3

III этап. Учебно-познавательная деятельность

Цель деятельности

Совместная деятельность

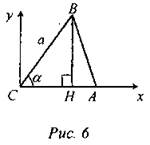
Доказать теорему о площади треугольника

(Г) Решите задачу.

Дано: ∆АВС ВС = а, АС = b, ∠C = α.

Найти: площадь треугольника.

Решение:

1. Координаты точки В равны: х = а ∙ cosα, y = b ∙ sinα.

2. Высота ВН = α ∙ sinα.

3.

Далее учащимся предлагается сверить свое решение и доказательство теоремы в учебнике на с. 256, сделать вывод

IV этап. Закрепление изученного материала

Цель деятельности

Совместная деятельность

При решении простейших задач отработать применение доказанной формулы

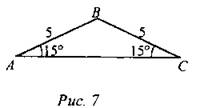
(Ф)

1. Решить на доске и в тетрадях задачи № 1020 (а), 1022, 1024.

2. Решить задачу: найти площадь равнобедренного треугольника с углом при основании 15° и боковой стороной 5 см.

Ответ: 25/4 см

V этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- По каким формулам можно вычислить площадь треугольника?

- Как найти синус угла прямоугольного треугольника?

- Составьте синквейн к уроку

(И) Домашнее задание: выучить теорему; решить № 1020 (б, в), 1021, 1023