Контрольные и самостоятельные работы по алгебре и геометрии 9 класс - 2016 год
САМОСТОЯТЕЛЬНЫЕ РАБОТЫ - Урок 2 - ГЕОМЕТРИЯ - ОТВЕТЫ
(по учебнику Л.С. Атанасяна и др.)
С1
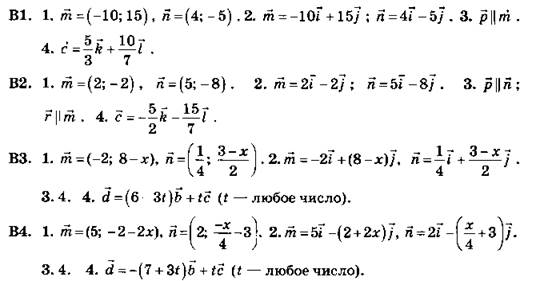
C2

![]()
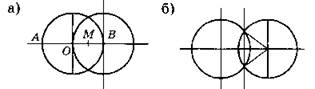
3. Указание. Достаточно показать, что координаты х, у точек А, В удовлетворяют заданному уравнению окружности.
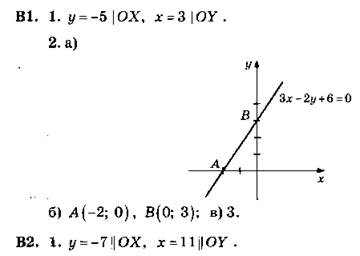
В2. 1.
![]()
3. Указание. Показать, что координаты х, у точек А, В удовлетворяют заданному уравнению окружности.
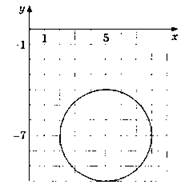
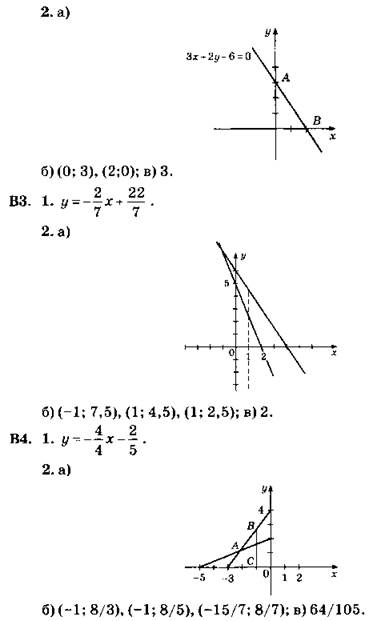
В3. 1. После выделения полных квадратов уравнение приводится к виду (x - 8)2 + (у + 2)2 = 10. Выделение полного квадрата осуществляется с помощью процесса:
![]()
В нашем случае ![]()
![]() (так как р = 16, р/2 = 8).
(так как р = 16, р/2 = 8).
Аналогично ![]() Отсюда
Отсюда
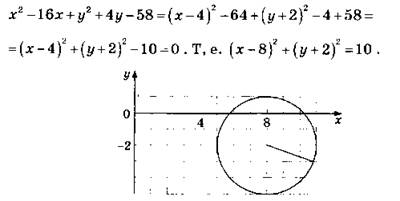
Радиус ![]() — строится как гипотенуза прямоугольного треугольника с катетами 3 клетки и 1 клетка (см. рис.).
— строится как гипотенуза прямоугольного треугольника с катетами 3 клетки и 1 клетка (см. рис.).
![]()
3. Ромб. ![]()
В4. 1. После выделения полных квадратов уравнение приводится к виду (х + 3)2 + (y - 7)2 = 3. Выделение полного квадрата осуществляется с помощью процесса:
![]()
![]()
В нашем случае ![]()
![]() (так как р = 6, р/2 = 3).
(так как р = 6, р/2 = 3).
Аналогично ![]() Отсюда
Отсюда
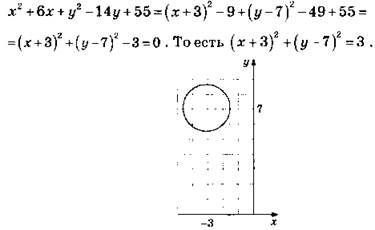
Радиус ![]() — строится как гипотенуза прямоугольного треугольника с катетами √2 (это диагональ клетки со стороной 1) и 1 клетка (см. рис.).
— строится как гипотенуза прямоугольного треугольника с катетами √2 (это диагональ клетки со стороной 1) и 1 клетка (см. рис.).
2. (х - 2)2+ (y + 1)2 = 25; (x - 1)2 + (y - 6)2= 25.
3. Ромб, (х - 2)2 + (у - 4)2 = 36/37.
С4
С5
![]()
3. Вычислить ![]() Показать, что
Показать, что ![]()
4. (6; 10/3).
5. 2.
![]()
3. Указание. Использовать равенства ![]()
![]()
C6
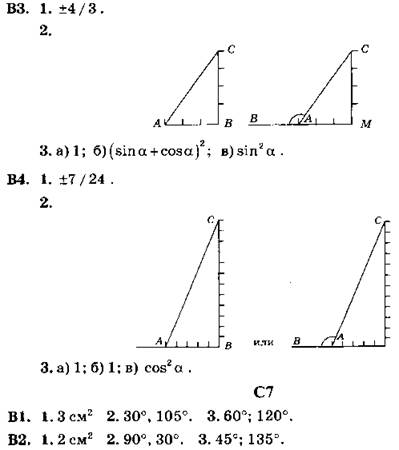
B1. 1. √3/2.
2. Так как cos А = 3/5 > 0, то угол А — острый. Поэтому ![]() Значит, откладываем катеты АВ = 3 — по горизонтали, ВС = 4 — по вертикали (прямоугольного треугольника АВС). Строим гипотенузу АС. Угол А построен.
Значит, откладываем катеты АВ = 3 — по горизонтали, ВС = 4 — по вертикали (прямоугольного треугольника АВС). Строим гипотенузу АС. Угол А построен.
![]()
В2. 1. 1/2.
2. Так как cos А = 12/13 > 0, то угол А — острый. Поэтому ![]() Следовательно, откладываем катеты АВ = 12 — по горизонтали, ВС = 5 — по вертикали прямоугольного треугольника АВС. Строим гипотенузу АС. Угол А построен.
Следовательно, откладываем катеты АВ = 12 — по горизонтали, ВС = 5 — по вертикали прямоугольного треугольника АВС. Строим гипотенузу АС. Угол А построен.
![]()
![]()
C8
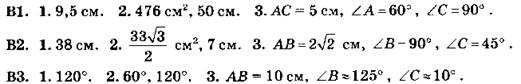
![]()
3. Из теоремы косинусов следует ![]() Из теоремы синусов получаем
Из теоремы синусов получаем ![]() поэтому
поэтому ![]() Зная синус острого угла, угол можно найти приблизительно — с помощью транспортира (намного точнее — с помощью калькулятора или таблицы Брадиса).
Зная синус острого угла, угол можно найти приблизительно — с помощью транспортира (намного точнее — с помощью калькулятора или таблицы Брадиса).
С9
С10 (дом.)
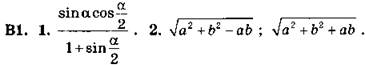
3. Указание. Выразить синусы углов из теоремы синусов. После подстановки этих выражений для синусов в требуемое равенство и исключения R получается равенство, выражающее теорему косинусов.
4. Положив ![]() выразить 4 вектора доказываемого равенства через векторы
выразить 4 вектора доказываемого равенства через векторы ![]() и показать, что
и показать, что ![]()
5. Положив ![]() выразить все 6 векторов равенства через
выразить все 6 векторов равенства через ![]() и вычислить левую часть равенства.
и вычислить левую часть равенства.
![]()
3. Выразить синусы углов из теоремы синусов. После подстановки этих выражений в требуемое равенство и исключения R получается равенство, выражающее теорему косинусов.
4. Положив ![]()
![]() выразить векторы доказываемого равенства через векторы
выразить векторы доказываемого равенства через векторы ![]() и, учитывая, что
и, учитывая, что ![]() показать, что
показать, что ![]()
5. Положив ![]() выразить все 6 векторов равенства через
выразить все 6 векторов равенства через ![]() и вычислить
и вычислить ![]()
С11

В3. 1. 28.
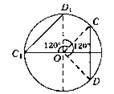
2. Указание. Применить теорему косинусов для равнобедренного треугольника с вершиной в центре, основанием а8 и углом при вершине ![]()
3. Указание. Применить формулы ![]()
B4. 1. 17.
2. Указание. Применить теорему косинусов для равнобедренного треугольника с вершиной в центре, основанием а12 и углом при вершине ![]()
3. Указание. Применить формулы ![]()
C12
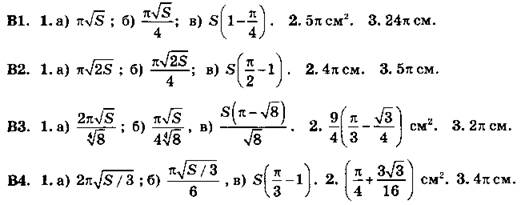
C13
B1. 1.
2. Три.
3. При осевой симметрии ![]()
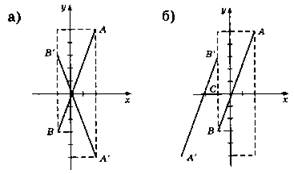
В2. 1.
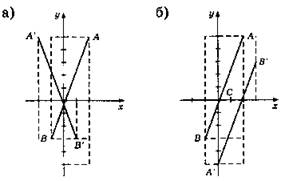
2. Четыре.
3. При осевой симметрии ![]()
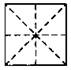
B3. 1.
2. Можно, если О — центр симметрии.
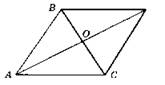
3.
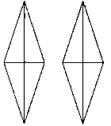
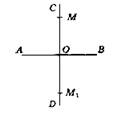
B4. 1.
2. Можно, ось симметрии ВК || АС.
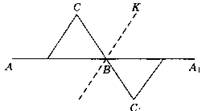
![]()
а' = а. Стороны равны. Треугольники равны, поэтому и углы равны.
C14
B1. 1.
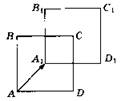
2.
![]()
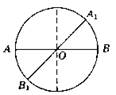
B2. 1.
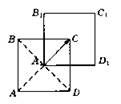
2.
![]()
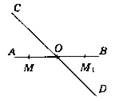
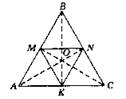
B3. 1. Проводим через точку А прямые, параллельные сторонам угла А. Точки К, Р — искомые.
![]()
2.
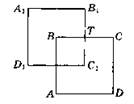
3. Пусть четырехугольник ABCD уже построен. Сделаем параллельный перенос отрезка АВ вправо на отрезок d. Получился отрезок DB1 = АВ. Продолжаем стороны АВ и DC до пересечения в точке Е. Проводим отрезок DF = АЕ. Тогда AEFD, ABB1D — параллелограмм. ∠CDF = а.
Теперь понятно, как построить четырехугольник.
Строим в точке D угол B1DC = а. На сторонах этого угла откладываем от вершины D отрезки DB1 = a, DC = с. Сторона CD построена. Точка В находится на расстоянии d от точки В1 и на расстоянии b от точки С. То есть на пересечении двух окружностей радиуса d и b соответственно. Точка А находится на расстоянии а от точки В и на расстоянии d от точки D, то есть как пересечение двух окружностей радиуса a и d соответственно.
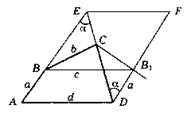
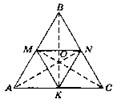
В4. 1. Проводим через точку А прямые, параллельные сторонам угла А. Точки К, Р — искомые.
![]()
2.
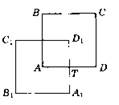
3. Пусть в четырехугольнике ABCD сумма углов А и В известна и равна φ. Тогда угол а = 180° - φ легко построить: продолжаем прямую MN за точку N.
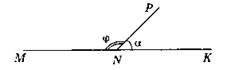
Угол а построен. Далее решение такое же, как в варианте 1.
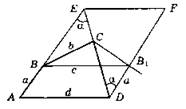
Строим в точке D угол B1DC = а. На сторонах этого угла откладываем от вершины D отрезки DB1 = a, DC = с. Сторона CD построена. Точка В находится на расстоянии d от точки В1 и на расстоянии b от точки С. То есть на пересечении двух окружностей радиуса d и b соответственно. Точка А находится на расстоянии а от точки В и на расстоянии d от точки D, то есть как пересечение двух окружностей радиуса and соответственно.