Контрольные и самостоятельные работы по алгебре и геометрии 9 класс - 2016 год
САМОСТОЯТЕЛЬНЫЕ РАБОТЫ - АЛГЕБРА - ОТВЕТЫ
С1
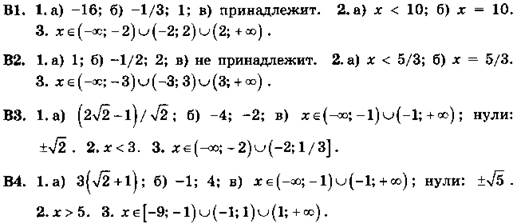
С2
В3. 1. Решение. Первый способ:
Так как ![]() при действительных корнях,
при действительных корнях,
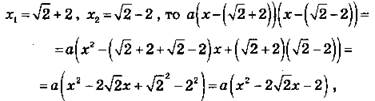
где а ≠ 0. При а = 1 получаем ответ: ![]()
Второй способ:
По теореме Виета
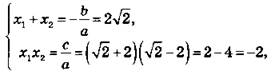
то при ![]() В общем виде
В общем виде ![]() Второй способ короче, но требует вспомнить теорему Виета.
Второй способ короче, но требует вспомнить теорему Виета.
![]()
В4. 1. Решение. Первый способ:
Так как ![]() при действительных корнях,
при действительных корнях, ![]() то
то
![]()
![]() где a ≠ 0. При a = 1 получаем ответ:
где a ≠ 0. При a = 1 получаем ответ: ![]()
Второй способ:
По теореме Виета
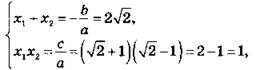
то при ![]() В общем виде
В общем виде ![]() Второй способ короче, но требует знания теоремы Виета.
Второй способ короче, но требует знания теоремы Виета.
![]()
С3
![]()
3.
![]()
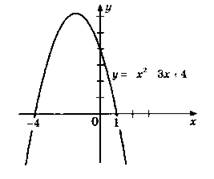
3.
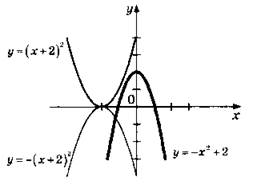
![]()
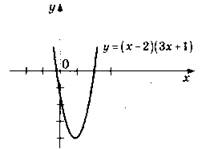
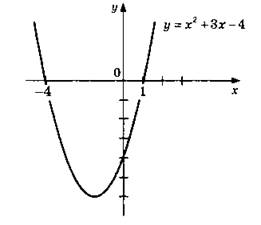
3. ![]() График параболы у = х2 сдвигаем вправо на две единицы, затем опускаем вниз на одну единицу. После этого часть полученного графика, которая оказалась ниже оси 0x, отражаем симметрично вверх относительно оси 0х. Растягиваем полученный график в три раза по оси ординат.
График параболы у = х2 сдвигаем вправо на две единицы, затем опускаем вниз на одну единицу. После этого часть полученного графика, которая оказалась ниже оси 0x, отражаем симметрично вверх относительно оси 0х. Растягиваем полученный график в три раза по оси ординат.
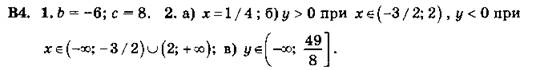
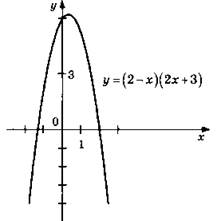
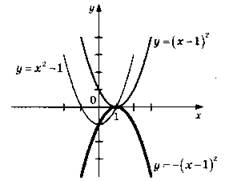
3. При ![]() График параболы у = х2 сдвигаем вправо на одну единицу, затем поднимаем вверх на одну единицу. После этого часть полученного графика, которая оказалась слева от оси 0у, стираем, а часть полученного графика, которая оказалась справа от оси 0у, отражаем симметрично влево относительно оси 0у. Растягиваем полученный график в три раза по оси ординат.
График параболы у = х2 сдвигаем вправо на одну единицу, затем поднимаем вверх на одну единицу. После этого часть полученного графика, которая оказалась слева от оси 0у, стираем, а часть полученного графика, которая оказалась справа от оси 0у, отражаем симметрично влево относительно оси 0у. Растягиваем полученный график в три раза по оси ординат.
*С4 (дом.)
![]()
![]()
7.
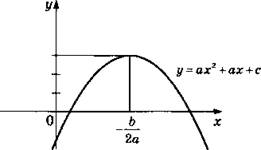
8. а) Возрастает на промежутках [-1,5; 0); [1,5; -∞). Убывает на промежутках (-∞; -1,5); [0; 1,5).
б) Возрастает на промежутках [1; 1,5); [2 ; +∞). Убывает на промежутках (-∞; 1); [1,5; 2).
![]()
![]()
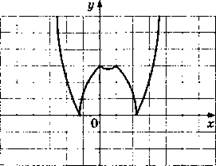
![]()
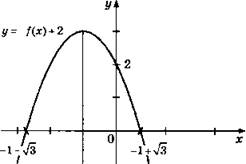
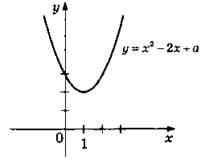
![]() Парабола у = -x2 сдвинута влево на 1 и поднята вверх на 3.
Парабола у = -x2 сдвинута влево на 1 и поднята вверх на 3.
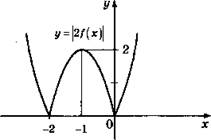
В параболе у = х2 + 2х = х(х + 2) график растягиваем в 2 раза по вертикали, а затем точки с отрицательными ординатами (в интервале (-2; 0)) отражаются симметрично относительно оси 0*.
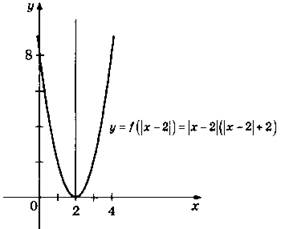
![]()
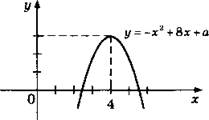
5. -1,8.
6. р — любое число.
7.
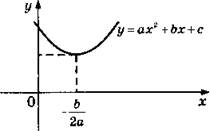
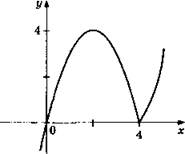
8. а) Возрастает на промежутках [-3,5; 0); [3,5; +∞). Убывает на промежутках (-∞; -3,5); [0; 3,5).
б) Возрастает на промежутках [2; 3,5); [5 ; +∞). Убывает на промежутках (-∞ ; 2); [3,5; 5).
![]()
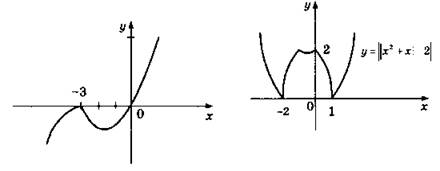
![]()
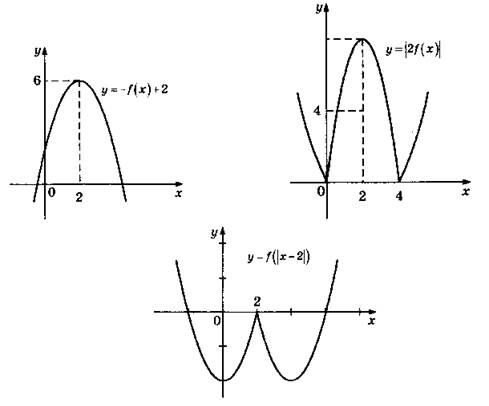
С5
![]() так как D < 0 и коэффициент при а2 равен 3 > 0.
так как D < 0 и коэффициент при а2 равен 3 > 0.
![]()
![]() так как D < 0 и коэффициент при а2 равен 4 > 0.
так как D < 0 и коэффициент при а2 равен 4 > 0.
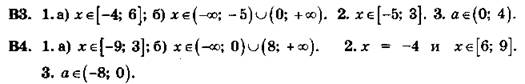
С6
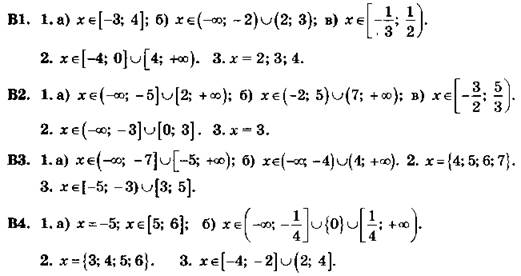
С7
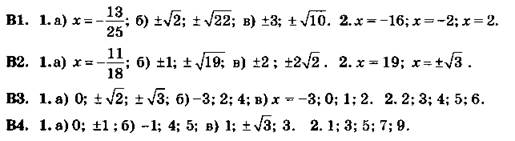
*С8 (дом.)
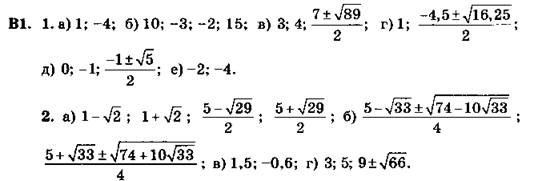
3. 1; -0,5 (Указание: дополнить до разности квадратов, добавив слева и справа ![]() затем сделать замену переменных
затем сделать замену переменных ![]() далее решаем квадратное уравнение).
далее решаем квадратное уравнение).
4. а) а = 0 (Указание: сделать замену переменных t = х2);
б) а > 0 (Указание: сделать замену переменных t = x2, далее анализировать квадратное уравнение).
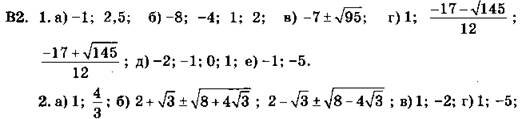
![]()
3. 1; -0,75 (Указание: сделать замену переменных ![]() затем решать квадратное уравнение).
затем решать квадратное уравнение).
4. а) а = 0; б) а > 0 (Указание: сделать замену переменных х2 = t, затем анализировать квадратное уравнение).
С9
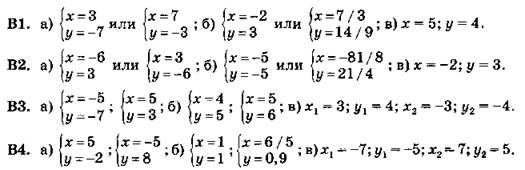
С10
B1. 1. (3; -2), (1; 0).
2. (6; 5); (-5; -6).
3. (0; 1), (1; 2).
В2. 1. (2; -1), (4; 3).
2. (4; 7).
3. (-1; 0), (2; 3).
В3. 1. (-6; -3); (-6; 3); (2; 1); (2; -1).
2. N = 36 (Указание: Обозначить число десятков неизвестного числа N через х, а число единиц через у и составить систему уравнений в соответствии с условиями задачи).
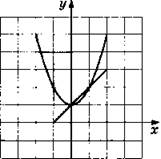
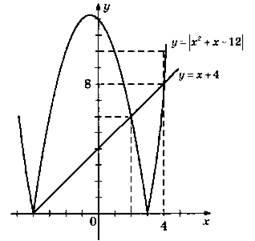
3. Указание: Изобразить на миллиметровке параболу и прямую, найти точки пересечения и записать приближенно их координаты. Ответ: (-2; 0), (2; 4); (4; 6).
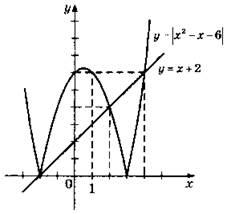
В4. 1. (3; -1), (3; 1), (-12; 4), (-12; -4).
2. N = 48 (Указание: Обозначить число десятков неизвестного числа N через х, а число единиц через у и составить систему уравнений в соответствии с условиями задачи).
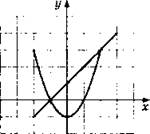
3. (-4; 0), (2; 6), (4; 8).
*C11
C12
C13
B1. 1. 40. 2. 8 км. 3. 210. 4. 268.
B2. 1. 20. 2. 4500 м. 3. 325. 4. 387.
В3. 1. -225. 2. 616. 3. n = 20; a1 = 2. 4. 95.
В4. 1. 312. 2. 585. 3. n = 10; а1 = 37. 4. 105.
C14
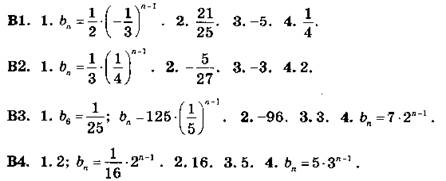
C15
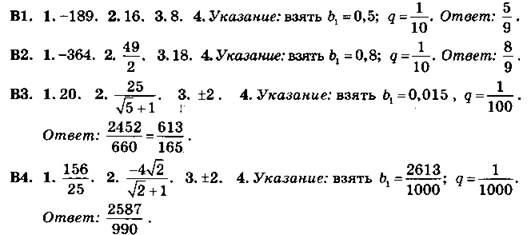
*C16 (дом.)
B1. 1. 2; 7; 12.
2. 1; 3; 9; 27.
3. 1; 2; 4; 6 и 6,25; 3,75; 2,25; 0,75.
4. 0,5.
В2. 1. 1; 3; 5 и 7; 3; -1.
2. 2; 4; 8; 16.
3. 0; 3; 6; 12 и 11,25; 6,75; 2,25; 0,75.
4. 1/3.
C17
B1. 1. Доказательство:
![]()
Следовательно, функция f(x) —нечетная, по определению.
![]()
2. Следовательно, функция g(x) — четная, по определению. Что и требовалось доказать.
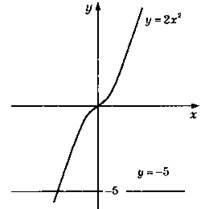
3. Нечетная.
4. Учесть значение (-1)n при n четных и нечетных.
а) Первое число больше; б) первое число меньше.
B2. 1. Доказательство:
![]()
Т.е. f(-х) = -f(х). Следовательно, функцияf(х) — нечетная, по определению.
![]()
Т. е. g(-х) = g(х). Следовательно, функция g(x) — четная, по определению. Что и требовалось доказать.
2. Два решения.
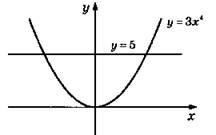
3. Четная. 4. Учесть значение (-1)n при n четных и нечетных.
а) Первое число меньше; б) первое число больше.
В3. 1. а) четная; б) функция общего вида, то есть не является четной и не является нечетной (так как х ≠ -5, но х = 5 допустим).
2. x1,2 = ±1.
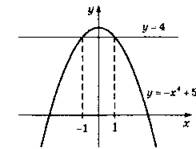
3.
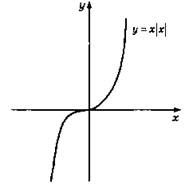
4. Нечетная.
В4. 1. а) четная; б) функция общего вида, то есть не является четной и не является нечетной (так как х ≠ 7, но х = -7 допустим).
2. x = -3.
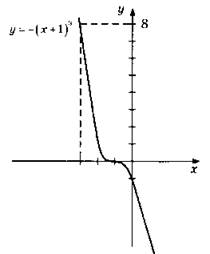
3.
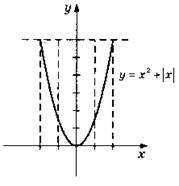
4. Четная.
С18
![]()
4. Указание: привести корни к единой степени. ![]()
![]()
4. Указание: привести корни к единой степени. ![]()
![]()
![]()
4. Указание: сравнить подкоренные числа. ![]() . Значит,
. Значит, ![]() Отсюда
Отсюда ![]()
![]()
4. Указание: привести корни к единой степени. ![]() .
. ![]()
*С19
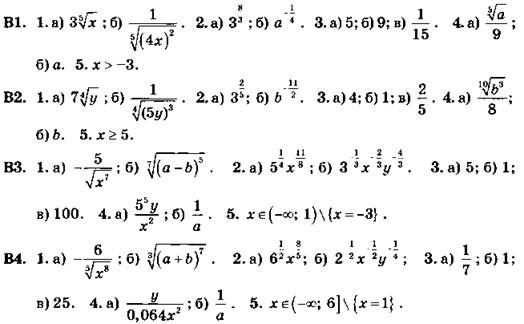
*С20
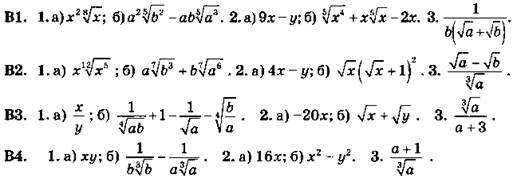
С21
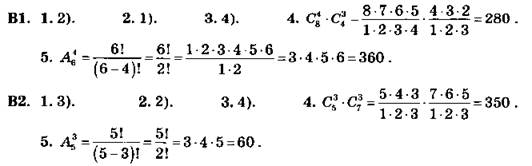
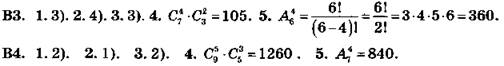
С22
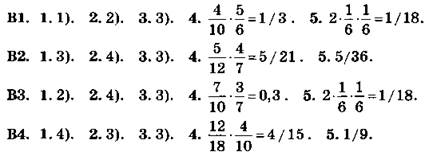
С23
В1. 1. 4). 2. 3). 3. 2). 4. 85%. 5. 1/6.
В2. 1. 1). 2. 4). 3. 3). 4. 85%. 5. 1/6.
В3. 1. 3). 2. 2). 3. 4). 4. 20%. 5. 5/36.
В4. 1. 2). 2. 2). 3. 4). 4. 80%. 5. 1/6.
*С24
![]()
4. Не может, так как ![]() Действительно,
Действительно, ![]()
![]()
4. Не может, так как ![]() Действительно,
Действительно, ![]()

*С25
![]()
2. а) Плюс; б) плюс.
![]()
4. Нет.
![]()
2. а) Минус; б) плюс.
3. a) -0,5; б) 1.
4. Да.
![]()
2. а) Плюс; б) минус.
![]()
4. Во II-й и III-й четверти.
![]()
2. а) Плюс; б) минус.
![]()
4. Во II-й и IV-й четверти.
*С26
![]()
3. а) Доказательство: Так как ![]() и sin2 a + cos2 a = 1 , to
и sin2 a + cos2 a = 1 , to
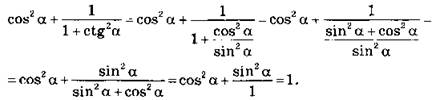
Что и требовалось доказать.
б) Доказательство:
![]()
![]()
Что и требовалось доказать.
![]()
3. Доказательство: а) Так как ![]() и sin2 a + cos2 a = 1 , то
и sin2 a + cos2 a = 1 , то
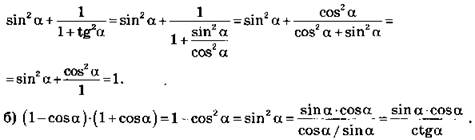
Что и требовалось доказать.
![]()
3. Доказательство:
а) Так как sin2 a + cos2 a = 1 , to
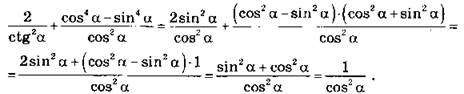
б) Так как tga = 1/ctg a, to
![]()
Что и требовалось доказать.
![]()
3.Доказательство: а) Так как ![]() и sin2 a + cos2 a = 1 , to
и sin2 a + cos2 a = 1 , to
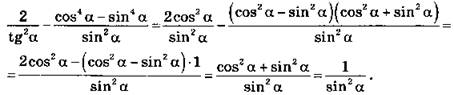
б) Так как ctg a = 1/tg a, to
![]()
Что и требовалось доказать.
*С27
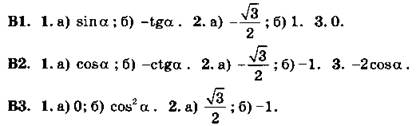
3.Доказательство: Используя формулы приведения и нечетность функции синус, получаем
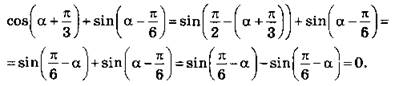
![]()
3. Доказательство:
*C28
![]()
3. По формуле приведения: ![]() ч.т.д.
ч.т.д.
![]()
3. По формуле приведения: ![]() ч.т.д.
ч.т.д.
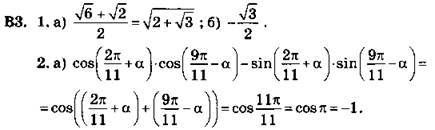
Так как ![]() ч.т.д.
ч.т.д.
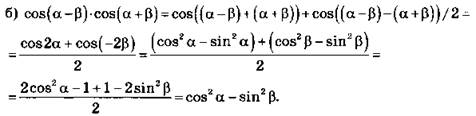
Так как ![]()
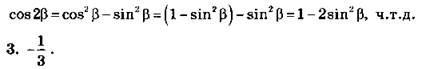
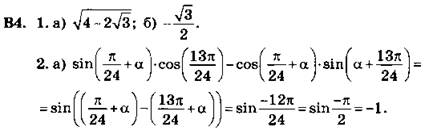
Так как ![]() ч.т.д. 3. 0,5.
ч.т.д. 3. 0,5.
*C29
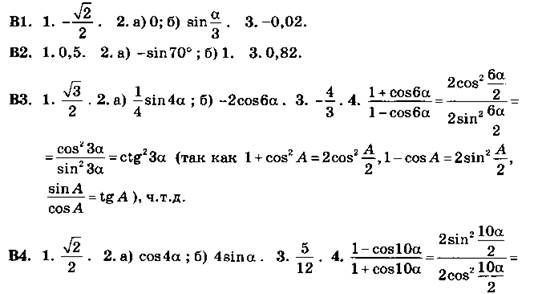
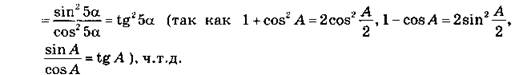
*C30

*C31 (дом.)
![]()
4. Доказательство:
![]()
Отсюда ![]() Так как
Так как ![]() то
то
![]()
![]()
Отсюда ![]() Поэтому
Поэтому
![]()
Что и требовалось доказать.
5. -3; -2; -1; 0; 1; 2; 3.
6. Доказательство: а) Так как ![]() то
то ![]()
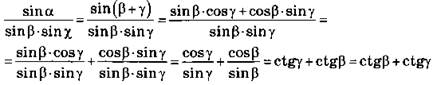
б) Так как ![]() то
то ![]() Тогда
Тогда
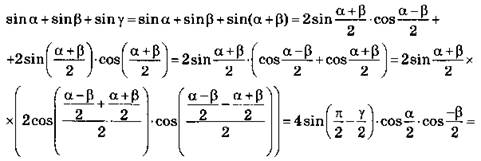
![]() Что и требовалось доказать.
Что и требовалось доказать.
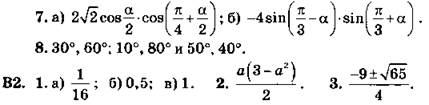
4. Доказательство:
![]()
![]()
Что и требовалось доказать.
5. -5; -4; -3; -2; -1; 0; 1; 2; 3; 4; 5.
6. Доказательство: а) Так как
![]()
![]()
![]() Что и требовалось доказать.
Что и требовалось доказать.
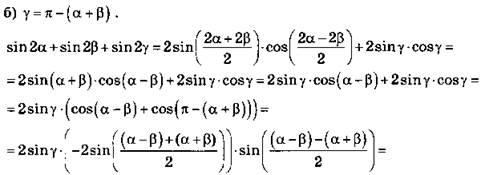
![]() Что и требовалось доказать.
Что и требовалось доказать.