Четные и нечетные функции. Функция у = xn - СТЕПЕНЬ ЧИСЛА - САМОСТОЯТЕЛЬНЫЕ РАБОТЫ - АЛГЕБРА

Вариант 1

1. Докажите, что функция f(x) является нечетной, а функция g(x) — четной, если

2. Постройте схематически график функции у = 2х³. С помощью графика определите, сколько решений имеет уравнение 2х³ = -5.

3. По данному графику определите, является ли данная функция четной или нечетной.

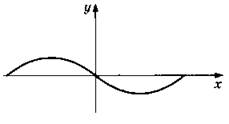
4. Сравните числа:

а) (-15)⁶ и (-12)⁶;

б) (-15)⁷ и (-12)⁷.

Вариант 2

1. Докажите, что функция f(x) является нечетной, а функция g(x) — четной, если

2. Постройте схематически график функции у = 3х⁴. С помощью графика определите, сколько решений имеет уравнение 3х⁴ = 5.

3. По данному графику определите, является ли данная функция четной или нечетной.

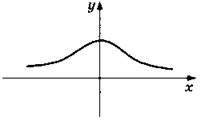
4. Сравните числа:

а) (-20)⁴ и (-24)⁴;

б) (-20)⁵ и (-24)⁵.

Вариант 3

1. Исследуйте функции на четность или нечетность:

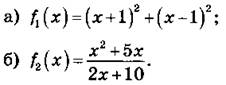
2. Постройте схематически график функции у = -х⁴ + 5. Пользуясь графиком, решите уравнение: -х⁴ + 5 = 4.

3. Используя свойства четности и нечетности функций, постройте график функции у = х |х|.

4. Известно, что f(x) — четная функция, g(x) — нечетная функция.

Определите, является ли четной или нечетной функция

Вариант 4

1. Исследуйте функции на четность или нечетность:

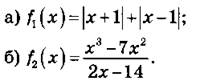
2. Постройте схематически график функции у = -(х + 1)³. Пользуясь графиком, решите уравнение: -(х + 1)³ = 8.

3. Используя свойства четности и нечетности функций, постройте график функции у = х² + |х|.

4. Известно, что f(x) — четная функция, g(x) — нечетная функция. Определите, является ли четной или нечетной функция