Алгебра поурочные планы 8 класс - по учебнику Ю. Н. Макарычева
РЕШЕНИЕ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙ - НЕРАВЕНСТВА
Цель: продолжить формирование умения решать неравенства с одной переменной путём перехода к равносильному неравенству.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Решите неравенство:
![]()
2. Назовите неравенство, множеством решений которого служит промежуток:
![]()
3. Какие из чисел -18; 10; 8; -3; 11 являются решениями неравенства 3х ≤ 24?
III. Актуализация знаний.
- Дайте определение решения неравенства с одной переменной.
- Что значит решить неравенство?
- Какие неравенства называются равносильными?
- Сформулируйте свойства равносильности неравенств, используемые при решении неравенства с одной переменной.
IV. Формирование умений и навыков.
Задания этого урока можно разбить на две группы:
1) Решение неравенств приведением к равносильному.
2) Составление неравенства по условию и последующее решение.
• Выполнение заданий: № 842 (а, в), 843 (а), 844.
№ 842.
а) Составим неравенство:
![]()
в) Составим неравенство:
![]()
Ответ: а) х > 0,5; в) с < -25.
№ 843.
а) Составим неравенство:
![]()
Ответ: при а < 2,5.
- Найдите наибольшее целое число, удовлетворяющее неравенству: ![]()
Решение
![]()
Наибольшее целое число х = 5.
![]()
![]()
Наибольшее целое число х = -16 (так как -15 не входит в данный открытый числовой луч).
![]()
Ответ: а) 5; б) -16.
№ 844.
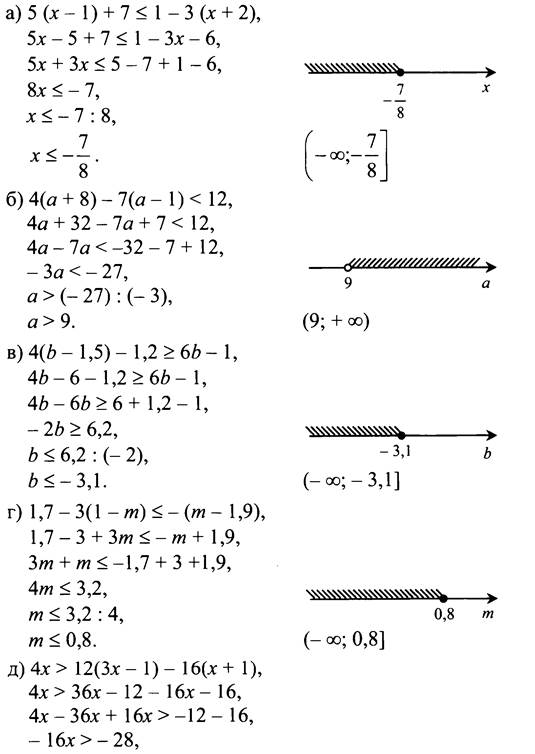

• № 846, № 847 (а, б), № 848 (а, б).
№ 846.
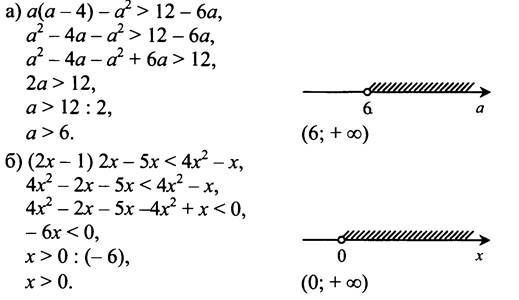
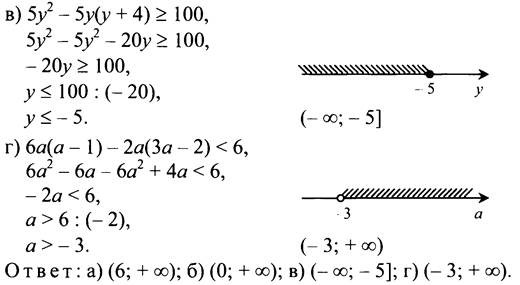
№ 847.
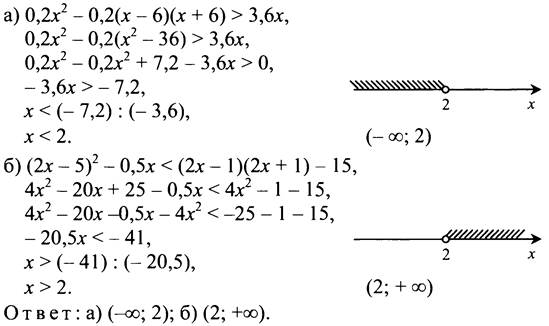
№ 848.
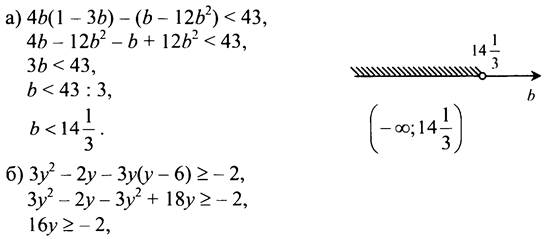
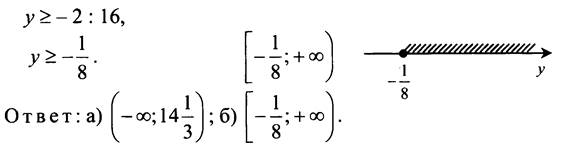
V. Итоги урока.
- Что значит решить неравенство с одной переменной?
- Какие преобразования приводят неравенство к равносильному?
- Какие виды записи решения неравенства существуют?
Домашнее задание: № 842 (б), 843 (б), 845, 847 (в, г), 848 (в, г), 871 (а).