Алгебра поурочные планы 8 класс - по учебнику Ю. Н. Макарычева
ДОКАЗАТЕЛЬСТВО ЧИСЛОВЫХ НЕРАВЕНСТВ - НЕРАВЕНСТВА
Цели: продолжить формирование умения доказывать числовое неравенство по его определению; формировать умение решать задачи на составление и доказательство числового неравенства.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Сравните числа а и b, если а - b равно:
![]()
2. Расположите в порядке возрастания числа: ![]()
3. Сравните числа:

III. Проверочная работа.
Вариант 1
Докажите неравенство:
![]()
Вариант 2
Докажите неравенство:
![]()
Решение заданий проверочной работы
Вариант 1
![]()
![]() значит, неравенство верно при любом значении у.
значит, неравенство верно при любом значении у.
![]()
![]() значит, неравенство верно при любом значении х.
значит, неравенство верно при любом значении х.
Вариант 2
![]()
![]() значит, неравенство верно при любом значении у.
значит, неравенство верно при любом значении у.
![]() значит, неравенство верно при любом значении х.
значит, неравенство верно при любом значении х.
IV. Формирование умений и навыков.
1. Разобрать пример 2 со с. 153-154 учебника.
2. Выполнить задания № 731 (а, в), 733,735 (б), 736 (а), 737.
№ 731.
![]() при любом значении а, значит, неравенство верное.
при любом значении а, значит, неравенство верное.
![]() при любых значениях b и с, значит, неравенство верное.
при любых значениях b и с, значит, неравенство верное.
№ 733.
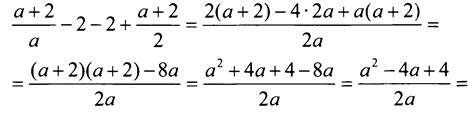
![]() при а > 0 (так как (а - 2)2 ≥ 0 и а > 0), значит, неравенство верное при любом положительном а.
при а > 0 (так как (а - 2)2 ≥ 0 и а > 0), значит, неравенство верное при любом положительном а.
№ 735.
![]() (так как
(так как ![]() ), значит, неравенство верное при любом значении с.
), значит, неравенство верное при любом значении с.
№ 736.
![]() при любом значении а.
при любом значении а.
№ 737.
Предложить выполнить по вариантам (4 варианта) и дать общий ответ.
![]() при любых значениях а.
при любых значениях а.
![]() при любых значениях а.
при любых значениях а.
![]() значит, не является верным при любом значении а.
значит, не является верным при любом значении а.
![]() при любых значениях а.
при любых значениях а.
Ответ: 3.
3. Выполнить задания № 738 (а, в), 739, 741.
Предлагаемые упражнения достаточно сложные и предполагают осознанное применение правила сравнения чисел.
№ 738.
Пусть а и b - положительные числа и а2 > b2. По определению а2 - b2 > 0. Разложим левую часть неравенства на множители (а - b)(а + b) > 0. Сомножитель а + b > 0 (так как а > 0 и b > 0), значит, и сомножитель а - b > 0, то есть а > b, что и требовалось доказать.
а) Составим разность квадратов чисел:
![]()
![]()
Значит, по доказанному выше свойству, ![]()
![]()
![]()
Значит, по доказанному выше свойству, ![]()
№ 739.
Это задание является продолжением предыдущего. Учащиеся могут вначале попытаться составить разность левой и правой части неравенства и определить её знак. Возникает проблемная ситуация. Затем можно предложить воспользоваться результатами решения предыдущей задачи, также следует задать учащимся вопрос о различиях в заданных ситуациях.
Составим разность квадратов выражений, стоящих в левой и правой частях неравенства
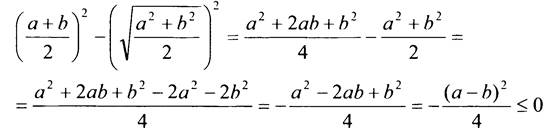 при любых а ≥ 0 и b ≥ 0. Значит, неравенство верно
при любых а ≥ 0 и b ≥ 0. Значит, неравенство верно 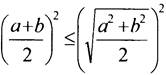 и верно
и верно 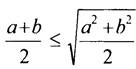 для любых а ≥ 0 и b ≥ 0.
для любых а ≥ 0 и b ≥ 0.
№ 741.
Даны числа 0; 1; 2; 3. Получили числа k: k + 1; k + 2; k + 3. Сравним произведения k ∙ (k + 3) и (k + 1) (k + 2). Составим разность этих выражений:
![]() значит,
значит, ![]() при любом значении k.
при любом значении k.
4. Сильным учащимся можно предложить для решения в классе или дома задачу повышенной трудности.
№ 742.
Анализ:
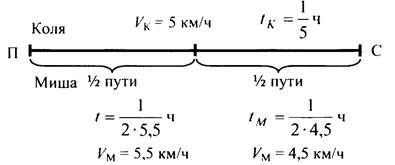
Сравним время, затраченное Колей и Мишей на путь от посёлка до станции. Составим разность
![]()
Значит, Коля затратил на путь меньше времени и пришёл на станцию раньше.
Ответ: Коля.
V. Итоги урока.
- Дайте определение числового неравенства.
- Сформулируйте универсальное правило сравнения двух чисел.
- Какие выражения называются средним арифметическим, средним геометрическим, средним гармоническим двух чисел? Каким соотношением они связаны?
Домашнее задание: № 735 (а), 736 (б), 738 (б, г), 740.