Алгебра поурочные планы 8 класс - по учебнику Ю. Н. Макарычева
УРАВНЕНИЕ С ПАРАМЕТРОМ - КВАДРАТНЫЕ УРАВНЕНИЯ
Цели: изучить понятие уравнение с параметром; сформировать умение решать линейные и квадратные уравнения с параметром.
Ход урока
I. Актуализация знаний.
Решить уравнения:
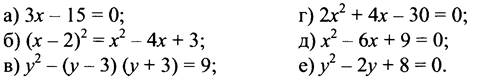
II. Изучение нового материала.
1. Изучение понятия “уравнение с параметром”.
Во время актуализации знаний учащиеся вспомнили, что линейное уравнение, в зависимости от коэффициентов, может иметь одно решение, бесконечно много решений либо не иметь решений. Так же квадратное уравнение, в зависимости от дискриминанта, а значит, от коэффициентов, может иметь один корень, два корня либо не иметь корней.
Если уравнение записано в виде равенства двух выражений, в запись которых входят две буквы, например ах = 5, то нужно четко определить, что это за уравнение. Различают три смысла:
1) х, а - равноценные переменные. Говорят, что задано уравнение с двумя переменными и требуется найти все пары (х, а), которые удовлетворяют данному уравнению.
2) х - переменная, а - фиксированное число. Говорят, что задано уравнение с одной переменной х и требуется найти значение х, удовлетворяющее уравнению при фиксированном значении а.
3) х - переменная, а - любое число из некоторого множества А. Говорят, что задано уравнение с переменной х и параметром а (А - множество изменения параметра) и требуется решить уравнение относительно х для каждого значения а.
Область изменения параметра либо оговаривается заранее, либо обычно подразумевается множество всех действительных чисел.
Тогда задачу решения уравнения с параметром можно переформулировать в задачу решения семейства уравнений, получаемых из уравнения при любых действительных значениях параметра.
2. Приём решения уравнения с параметром.
Ясно, что выписать каждое уравнение из бесконечного семейства уравнений невозможно. Тем не менее каждое уравнение семейства должно быть решено. Сделать это можно, если по некоторому целесообразному признаку разбить множество всех значений параметра на подмножества и решить затем заданное уравнение на каждом из этих подмножеств.
Для разбиения множества значений параметра на подмножества удобно воспользоваться теми значениями параметра, при которых или при переходе через которые происходят качественныеизменения уравнения. Такие значения параметра называются контрольными.
3. Алгоритм решения уравнения с параметром:
1-й шаг. Находим область изменения параметра.
2-й шаг. Находим ОДЗ уравнения.
3-й шаг. Определяем контрольные значения параметра и разбиваем область изменения параметра на подмножества.
4-й шаг. Решаем уравнение на каждом подмножестве области изменения параметра.
5-й шаг. Записываем ответ.
4. Решение линейных и квадратных уравнений с параметром.
На примерах со с. 141-143 учебника рассмотреть, как обнаруживаются контрольные значения параметра, как с их помощью множество значений параметра разбивается на подмножества и как затем на каждом из подмножеств решается заданное линейное или квадратное уравнение.
III. Формирование умений и навыков.
Все упражнения, относящиеся к этому пункту, можно разбить на 3 группы:
1) решить уравнение с параметром, заданное в стандартном виде: № 641;
2) преобразовать уравнение с параметром и решить его: № 642, 644;
3) найти значения параметра, при которых будет выполняться некоторое условие: № 646.
• Выполнение упражнений по учебнику.
№ 641 (а).
py – p - 1 = 0
Если р = 0, то уравнение примет вид: -1 = 0.
Данное уравнение не имеет корней.
Если р ≠ 0, то ру = р + 1; ![]()
Ответ: при р = 0 нет корней; при р ≠ 0 ![]()
№ 642.
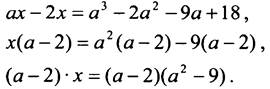
Если а - 2 = 0, то есть а = 2, то
![]()
х - любое.
Если а - 2 ≠ 0, то есть а ≠ 2, то
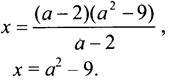
Ответ: при а = 2х - любое; при а ≠ 2 х = а2 - 9.
№ 644 (б).
![]()
Если а = 0, то D = 0 и ![]()
Если а ≠ 0, то D > 0 и
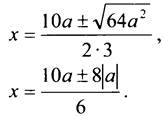
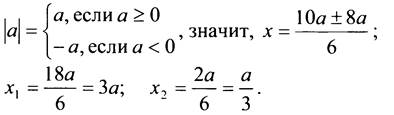
Ответ: при а = 0, х = 0; при а ≠ 0, х1 = 3а, х2 = а/3.
№ 646.
![]() при любом а, 2 корня.
при любом а, 2 корня.
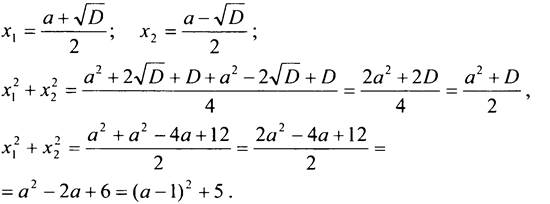
![]() принимает наименьшее значение при а = 1 и равно 5.
принимает наименьшее значение при а = 1 и равно 5.
Ответ: 5 при а = 1.