Алгебра поурочные планы 8 класс - по учебнику Ю. Н. Макарычева
КОНТРОЛЬНАЯ РАБОТА 5 - КВАДРАТНЫЕ УРАВНЕНИЯ
Вариант 1
1. Решите уравнение:
![]()
2. Периметр прямоугольника равен 20 см. Найдите его стороны, если известно, что площадь прямоугольника равна 24 см2.
3. В уравнении х2 + рх - 18 = 0 один из его корней равен - 9. Найдите другой корень и коэффициент р.
Вариант 2
1. Решите уравнение:
![]()
2. Периметр прямоугольника равен 30 см. Найдите его стороны, если известно, что площадь прямоугольника равна 56 см2.
3. Один из корней уравнения х2 + 11x + q = 0 равен - 7. Найдите другой корень и свободный член q.
Вариант 3
1. Решите уравнение:
![]()
2. Периметр прямоугольника равен 26 см, а его площадь 36 см2. Найдите длины сторон прямоугольника.
3. В уравнении х2 + рх + 56 = 0 один из его корней равен - 4. Найдите другой корень и коэффициент р.
Вариант 4
1. Решите уравнение:
![]()
2. Периметр прямоугольника равен 22 см, а его площадь 24 см2. Найдите длины сторон прямоугольника.
3. Один из корней уравнения х2 - 7х + q = 0 равен 13. Найдите другой корень и свободный член q.
Решение вариантов контрольной работы
Вариант 1
1. а) 2х2 + 7х - 9 = 0.
1-й способ. ![]() 2 корня.
2 корня.
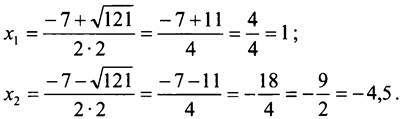
2- й способ. а + b + с = 0, значит, ![]() то есть
то есть ![]()
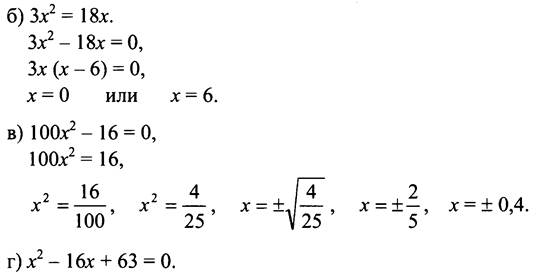
1-й способ. ![]() 2 корня.
2 корня.
![]()
2-й способ. По теореме, обратной теореме Виета, имеем: х1 + x2 = 16, x1 ∙ х2 = 63. Подбором получаем x1 = 9, х2 = 7.
Ответ: а) -4,5; 1; б) 0; 6; в) ±0,4; г) 7; 9.
2. Пусть х см - одна сторона прямоугольника, тогда вторая сторона ![]() см, что составляет (10 - х) см. Зная, что площадь прямоугольника равна 24 см2, составим уравнение:
см, что составляет (10 - х) см. Зная, что площадь прямоугольника равна 24 см2, составим уравнение:
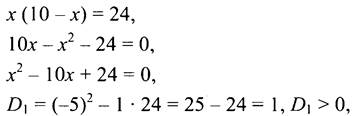 2 корня.
2 корня.
![]()
Оба корня удовлетворяют условию задачи.
Ответ: 4 см; 6 см.
3. Пусть x1 = -9 и x2 — корни уравнения х2 + рх - 18 = 0, тогда по теореме Виета -9 + х2 = -p и -9 ∙ х2 = -18.
Имеем: ![]() отсюда р = 7.
отсюда р = 7.
Ответ: х2 = 2; р = 7.
Вариант 2
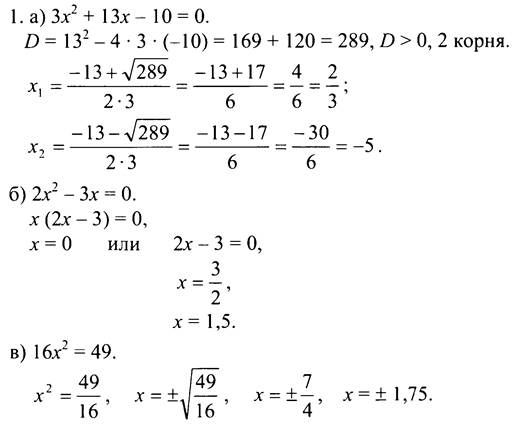
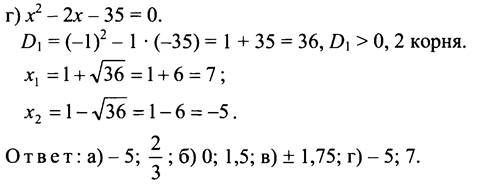
2. Пусть х см - одна сторона прямоугольника, тогда вторая сторона ![]() см, что составляет (15 - х) см. Зная, что площадь прямоугольника равна 56 см2, составим уравнение:
см, что составляет (15 - х) см. Зная, что площадь прямоугольника равна 56 см2, составим уравнение:
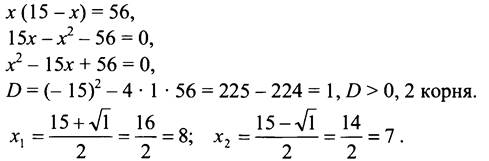
Оба корня удовлетворяют условию задачи.
Ответ: 7 см; 8 см.
3. Пусть x1 = -7 и x2 - корни уравнения х2 + 11x + q = 0, тогда по теореме Виета, -7 + х2 = -11 и -7 ∙ х2 = q.
Имеем: х2 = -11 + 7, х2 = -4 и - 7 ∙ (-4) = q, отсюда q = 28.
Ответ: х2 = -4; q = 28.
Вариант 3
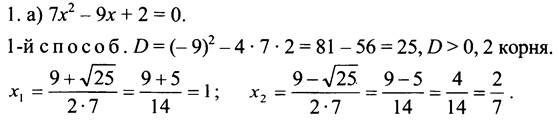
2-й способ. a + b + с = 0, значит, x1 = 1, х2 = c/a, то есть x1 = 1, х2 = 2/7.
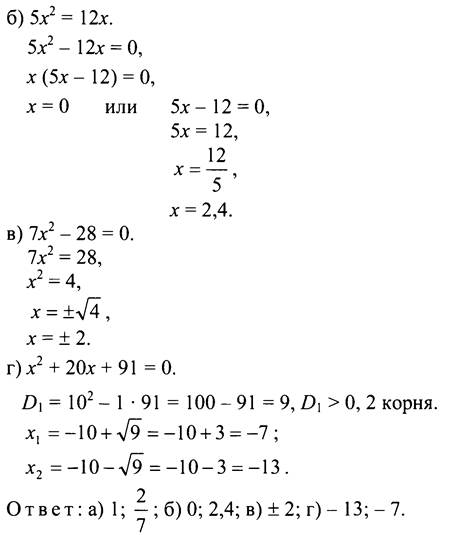
2. Пусть х см - одна сторона прямоугольника, тогда вторая сторона ![]() см, что составляет (13 - х) см. Зная, что площадь прямоугольника равна 36 см2, составим уравнение:
см, что составляет (13 - х) см. Зная, что площадь прямоугольника равна 36 см2, составим уравнение:
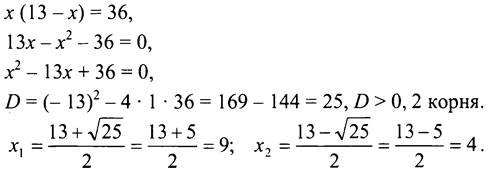
Оба корня удовлетворяют условию задачи.
Ответ: 4 см; 9 см.
3. Пусть х1 = -4 и х2 - корни уравнения х2 + рх + 56 = 0, тогда по теореме Виета -4 + х2 = -р и -4 ∙ х2 = 56.
Имеем: х2 = 56/-4; x2 = -14 и -4 + (-14) = -р, отсюда p = 18.
Ответ: x2 = -14; р = 18.
Вариант 4
1. а) 9x2 - 7х - 2 = 0.
1-й способ. ![]() 2 корня.
2 корня.
![]()
2-й способ. а + b + с = 0, значит, x1 = 1, х2 = c/a, то есть x1 = 1, х2 = -2/9.
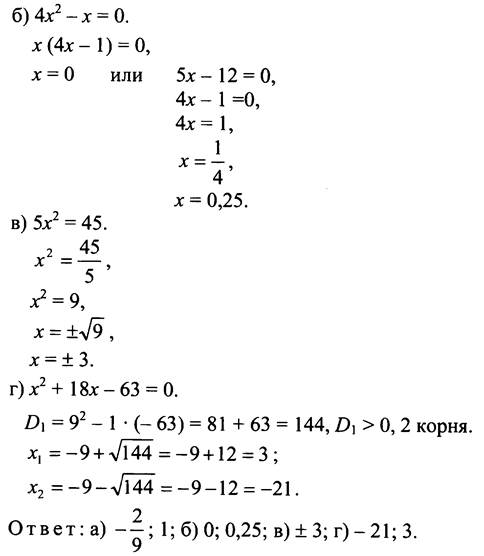
2. Пусть х см - одна сторона прямоугольника, тогда вторая сторона ![]() см, что составляет (11 - х) см. Зная, что площадь прямоугольника равна 24 см2, составим уравнение:
см, что составляет (11 - х) см. Зная, что площадь прямоугольника равна 24 см2, составим уравнение:
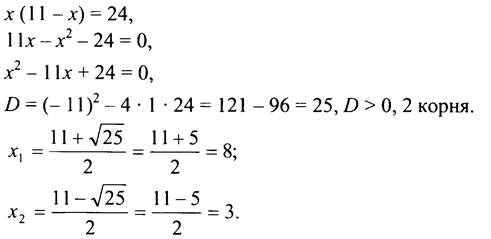
Оба корня удовлетворяют условию задачи.
Ответ: 3 см; 8 см.
3. Пусть x1 = 13 и x2 - корни уравнения х2 - 7х + q = 0, тогда, по теореме Виета, 13 + x2 = 7 и 13 ∙ x2 = q.
Имеем: х2 = 7 - 13, х2 = -6 и 13 ∙ (-6) = q, отсюда q = -78.
Ответ: x2 = -6; q = -78.