Алгебра поурочные планы 8 класс - по учебнику Ю. Н. Макарычева
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ КВАДРАТНЫХ УРАВНЕНИЙ - КВАДРАТНЫЕ УРАВНЕНИЯ
Цель: продолжить формирование умения решать текстовые задачи с помощью составления квадратных уравнений.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Найдите дискриминант квадратного уравнения и определите, сколько корней имеет уравнение:
![]()
2. Решите уравнение:
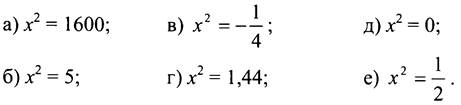
III. Формирование умений и навыков.
№ 570.
Пусть х - число обезьян в стае, тогда ![]() обезьян спряталось в гроте. Зная, что на виду осталась одна обезьяна, составим уравнение:
обезьян спряталось в гроте. Зная, что на виду осталась одна обезьяна, составим уравнение:
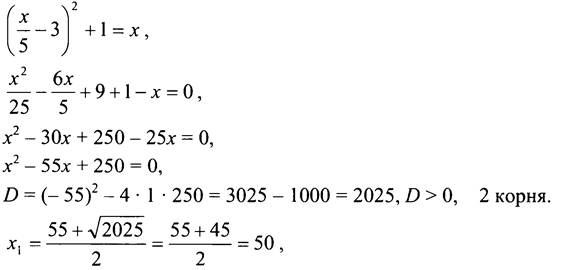
![]()
не удовлетворяет условию задачи, так как x/5 - 3 в этом случае - отрицательное число.
Ответ: 50 обезьян.
№ 571.
Пусть х - количество сторон в выпуклом многоугольнике, тогда (х + 25) - количество диагоналей в нём. Зная, что количество диагоналей (р) связано с количеством сторон (n) по формуле ![]() составим уравнение:
составим уравнение:
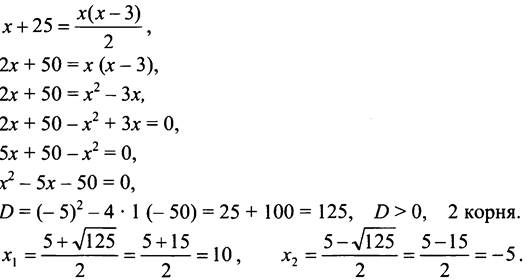
Так как х выражает число сторон многоугольника, то это не может быть отрицательное число, значит, x2 = -5 не удовлетворяет условию задачи.
Ответ: в десятиугольнике.
№ 573.
При решении этой задачи используются элементы комбинаторики, поэтому следует разобрать её с учителем.
Решение
Пусть х - количество участников турнира, тогда каждый участник играл с (х - 1) участником. Количество комбинаций равно х(x - 1). Но так как в комбинации участвует два человека, а партия одна, то число партии равно ![]()
Зная, что всего было сыграно 45 партий, составим уравнение:
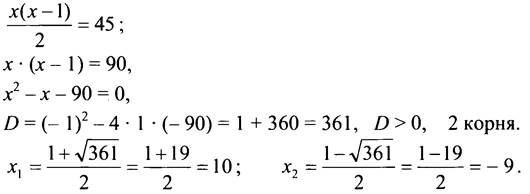
Так как х выражает количество участников турнира, то это не может быть отрицательное число, значит, х2 = -9 не удовлетворяет условию задачи.
Ответ: 10 участников.
№ 575.
Пусть х, (х + 1), (х + 2) - три последовательных целых числа. Зная, что сумма их квадратов равна 869, составим уравнение:
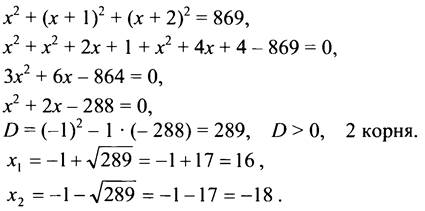
Оба корня удовлетворяют условию задачи, значит, это последовательные числа 16; 17; 18 или -18; -17; -16.
Ответ: 16; 17; 18 или -18; -17; -16.
IV. Проверочная работа.
Решите задачи:
Вариант 1
1. Два последовательных чётных числа таковы, что квадрат большего из них в 9 раз больше меньшего числа. Найдите эти числа.
2. Одну сторону квадрата уменьшили на 2 см, а другую - на 1 см и получили прямоугольник с площадью 6 см2. Найдите длину стороны квадрата. Изобразите квадрат и прямоугольник.
Вариант 2
1. Два последовательных нечётных числа таковы, что квадрат большего из них в 9 раз больше меньшего числа. Найдите эти числа.
2. Одну сторону квадрата увеличили на 2 см, а другую - на 1 см и получили прямоугольник с площадью 12 см2. Найдите длину стороны квадрата. Изобразите квадрат и прямоугольник.
Примечание. В зависимости от уровня подготовки класса можно сократить содержание проверочной работы до одной задачи.
Пример выполнения проверочной работы:
Вариант 1
1. Пусть х и (х + 2) - два последовательных чётных числа. Зная, что квадрат большего из них в 9 раз больше меньшего числа, составим уравнение:
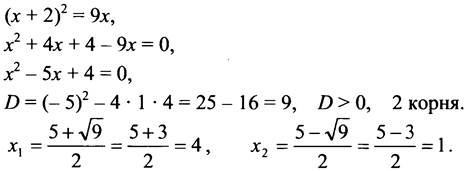
Так как число - чётное, то x2 = 1 - не удовлетворяет условию задачи.
Ответ: 4; 6.
2. Пусть х см сторона квадрата, тогда (х - 2) см и (х - 1) см - стороны прямоугольника. Зная, что площадь полученного прямоугольника равна 6 см, составим уравнение:
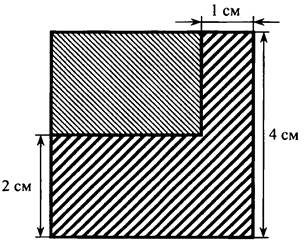
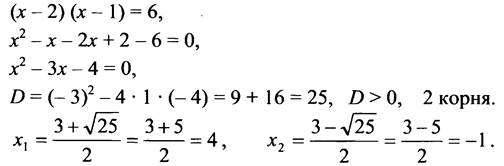
Так как сторона квадрата выражается положительным числом, то x2 = -1 - не удовлетворяет условию задачи.
Ответ: 4 см.
Вариант 2
1. Пусть х и (х + 2) - два последовательных нечётных числа. Зная, что квадрат большего из них в 9 раз больше меньшего числа, составим уравнение:
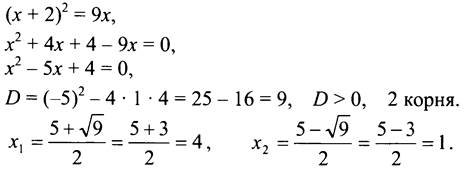
Так как число - нечётное, то х1 = 4 - не удовлетворяет условию задачи.
Ответ: 1; 3.
2. Пусть х см - сторона квадрата, тогда (х + 2) см и (х + 1) см - стороны прямоугольника. Зная, что площадь полученного прямоугольника равна 12 см, составим уравнение:
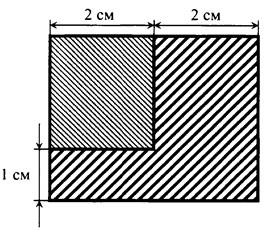
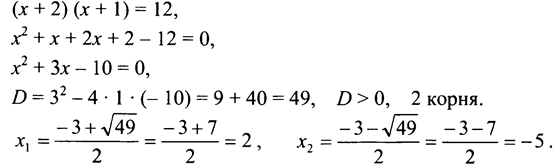
Так как сторона квадрата выражается положительным числом, то x2 = -5 - не удовлетворяет условию задачи.
Ответ: 2 см.
V. Итоги урока.
- Какие этапы выделяют при решении задачи алгебраическим методом?
- В чём состоит интерпретация полученного решения задачи?
- Когда полученное решение может противоречить условию задачи?
- Какие решения, полученные на сегодняшнем уроке, вы интерпретировали как противоречащие условию задачи?
Домашнее задание: № 569, 572, 574, 578 (б).