ТРАПЕЦИЯ - ЧЕТЫРЕХУГОЛЬНИКИ

Цель деятельности учителя

Создать условия для введения понятий “трапеция”, “равнобокая трапеция”, “прямоугольная трапеция”; для рассмотрения решения задач, в которых раскрываются свойства трапеции

Термины и понятия

Трапеция, основания трапеции, боковые стороны

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют объяснять, какой многоугольник называется трапецией, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии

Познавательные: проводят информационно-смысловой анализ текста и лекции; осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, умением устанавливать причинно-следственные связи.

Регулятивные: принимают и сохраняют учебную задачу.

Коммуникативные: умеют применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач, работать в группе.

Личностные: умеют контролировать процесс и результат учебной математической деятельности

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И); групповая (Г)

Образовательные

ресурсы

• Учебник.

• Задания для индивидуальной работы

I этап. Проверка домашнего задания

Цель деятельности

Совместная деятельность

Выявить трудности, возникшие при выполнении домашнего задания

(Ф) 1. Сформулируйте и докажите теорему Фалеса.

2. Сформулируйте свойства параллелограмма.

3. Сформулируйте признаки параллелограмма

II этап. Учебно-познавательная деятельность

Изучение нового материала

Цель деятельности

Совместная деятельность

Ввести понятие трапеции, ее оснований и боковых сторон

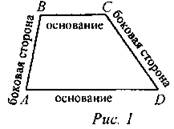
(Ф/И) 1. В тетрадях учащихся и на доске Picture трапеции и записи:

ABCD - трапеция, если ВС || AD, АВ и CD - боковые стороны, ВС и AD основания.

2. Ввести понятия равнобедренной и прямоугольной трапеции.

Учебно-исследовательская деятельность

Цель деятельности

Деятельность учителя

Деятельность учащихся

Сформулировать свойства равнобедренной трапеции

(Г) Класс разбивается на несколько групп для обсуждения свойств и признаков равнобедренной трапеции.

Задание: исследовать углы равнобедренной трапеции, диагонали трапеции.

Результаты исследований выслушать и обсудить, на доске и в тетрадях выполнить запись:

Свойства равнобедренной трапеции:

1. В равнобедренной трапеции углы при каждом основании равны.

2. В равнобедренной трапеции диагонали равны.

Задание: сформулируйте утверждения, обратные свойствам равнобедренной трапеции, и докажите их справедливость. Результаты исследований выслушать и обсудить, на доске и в тетрадях выполнить запись:

1. Если углы при основании трапеции равны, то она равнобедренная.

2. Если диагонали трапеции равны, то она равнобедренная.

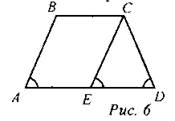
1. Доказательство:

Проведем СЕ || АВ.

АВСЕ - параллелограмм (АВ || СЕ, ВС || АD).

CD = AB = СЕ, ∆CDE -равнобедренный, ∠1 = ∠2.

АВ || СЕ, тогда ∠2 = ∠3. ∠1= ∠2 = ∠3.

∠ABC = 180° - ∠3 = 180° -∠1 = ∠BCD

2. Доказательство:

∆АВС = ∆DCB (АВ = DC, ВС - общая сторона, ∠ABC =∠DCB), тогда АС = BD.

3. Доказательство:

Проведем СЕ || АВ.

АВСЕ - параллелограмм, тогда АВ = СЕ, ∠A = ∠CED.

∆CED - равнобедренный(∠D = ∠CED), тогда СЕ =CD.

АВ = СЕ = CD, тогда ABCD - равнобедренная трапеция.

4. Доказательство:

Проведем СК || BD.

BCKD - параллелограмм (СК || BD, ВС || АК).

∆АСК- равнобедренный (АС = BD = СК), ∠1 = ∠2.

СК || BD, ∠2 = ∠3, тогда ∠1= ∠3.

∆ABD = ∆DCA (АС - BD, AD- общая сторона, ∠1 = ∠3),тогда АВ = CD, то естьABCD - равнобедренная трапеция

III этап. Решение задач

Цель деятельности

Обучающие и развивающие задания и упражнения

Диагностические задания

Ввести понятие средней линии трапеции

(Ф) № 386 (по теореме Фалеса). После решения этой задачи можно дать определение средней линии трапеции.

М- середина АВ, N - середина CD, MN - средняя линия трапеции

№ 386.

Доказательство:

Пусть М - середина АВ. ПроведемMN || AD || ВС. Точка N - середина CD (по теореме Фалеса). Докажем, что MN -единственная. Через точки М и Nможно провести только одну прямую (по аксиоме), то есть отрезок, соединяющий середины боковых сторон, единственен иMN || AD || ВС

IV этап. Итоги урока

Деятельность учителя

Деятельность учащихся

(Ф) 1. Какой четырехугольник называется трапецией?

2. Назовите элементы трапеции и ее виды.

3. В решении задач на трапецию можно использовать свойства углов при параллельных прямых и секущей

V этап. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И) 1. Оцените свою работу на уроке.

2. Какой этап урока вызвал у вас наибольшее затруднение и почему?

3. Составьте синквейн к уроку

(И) Домашнее задание: выучить теоретическую часть; решить № 384, 387