Геометрия 8 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
ПЛОЩАДЬ МНОГОУГОЛЬНИКА - Урок 2 - ПЛОЩАДЬ
|
Цель деятельности учителя |
Создать условия для выведения формулы площади прямоугольника |
||||
|
Термины и понятия |
Равновеликие многоугольники, равносоставленные многоугольники, площадь квадрата, площадь прямоугольника |
||||
|
Планируемые результаты |
|||||
|
Предметные умения |
Универсальные учебные действия |
||||
|
Владеют базовым понятийным аппаратом по основным разделам содержания; имеют представление об основных изучаемых понятиях |
Познавательные: умеют выбирать и создавать алгоритмы для решения математических проблем. Регулятивные: умеют самостоятельно ставить цели, адекватно оценивать правильность или ошибочность выполнения учебной задачи. Коммуникативные: умеют находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики |
||||
|
Организация пространства |
|||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||||
|
Образовательные ресурсы |
• Учебник. • Задания для фронтальной и индивидуальной работы |
||||
|
I этап. Проверка домашнего задания |
|||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|||
|
Выявить трудности, возникшие у учащихся при выполнении домашней работы |
(Ф) 1. Ответить на вопросы учащихся. 2. Проверить решение № 448 |
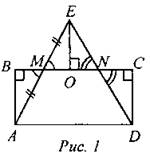
№ 448.
Решение: Опустим перпенпикупяр к BC из точки E (ЕО ⊥ PC). Прямоугольные треугольники АВМ и ЕОМ равны по гипотенузе и острому углу (АМ = ЕМ, ∠BMA = ∠EMO), отсюда ЕО = АВ, значит, ЕО = СD, так как в прямоугольнике противолежащие стороны АВ иCD равны. Прямоугольные треугольники EON и DCN равны по катету и острому углу (ЕО = CD, ∠ONE = ∠CND, как вертикальные). SAED = SANMD + SMOE + SNOE, ∆МОЕ = ∆МВА => SMOE = SMBA, ∆NОЕ = ∆NCD => SMOE = SNCD. Тогда SAED = SANMD + SMBA + SNCD = SABCD, ч. т. д. |
|||
|
II этап. Изучение нового материала |
|||||
|
Цель деятельности |
Совместная деятельность |
||||
|
Доказать формулу площади прямоугольника |
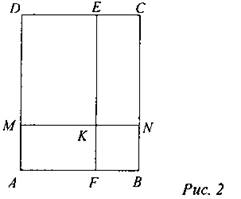
(Ф/И) Выполните задания: 1. Докажите, что два прямоугольника равны, если равны их смежные стороны. 2. ABCD - квадрат, MN || АВ, EF || ВС. Найдите площадь четырехугольника AFKM, если AM = СЕ = 3 см, DE = 6 см.
3. Доказать теорему о площади прямоугольника. (Подготовить чертеж заранее, см. учебник, рис. 181.) |
||||
|
III этап. Закрепление изученного материала |
|||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|||
|
Отработать умение применять формулу площади прямоугольника |
(Ф/И) 1. Решить № 452 (а, в), 453 (в) (устно). 2. Решить задачу № 458 на доске и в тетрадях учащихся. Один из учащихся решает задачу у доски, остальные в тетрадях |
№ 458.
Заборы имеют одинаковую длину, поэтому участки земли имеют одинаковый периметр.
36 100 м2 > 35 200 м2, поэтому площадь квадрата больше площади прямоугольника. 36 100 - 35 200 = 900 (м2) Ответ: площадь участка земли, имеющего форму квадрата, больше на 900 м2 |
|||
|
IV этап. Самостоятельная работа |
|||||
|
Цель деятельности |
Задания для самостоятельной работы |
||||
|
Закрепить полученные знания |
(И) Самостоятельная работа (5-7 минут) с последующей самопроверкой. 1. Найдите площадь прямоугольника, если его периметр равен 80 см, а отношение сторон равно 2:3.
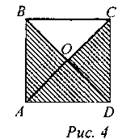
Решение: х - коэффициент пропорциональности. Р = 2х + 3х + 2х + 3х = 80; х = 8 АВ = 16 см, AD = 24 см. S = 16 ∙ 24 = 384 (см2) Ответ: 384 см2. 2. Площадь пятиугольника АВOСD равна 48 см2. Найдите площадь и периметр квадрата ABCD.
Решение: SABO = SADO = SCDO = SBOC SABPCD = 48 см2, SABO = 16 см2, SABCD = 64 см2, тогда АВ = 8 см, PABCD = 32 см. Ответ: 64 см2, 32 см |
||||
|
V этап. Итоги урока. Рефлексия |
|||||
|
Деятельность учителя |
Деятельность учащихся |
||||
|
(Ф) - Что нового узнали на уроке? - Сформулируйте 3 вопроса по сегодняшней теме |
(И) Домашнее задание: вопрос 3, с. 133; № 452 (б, г), 453 (а, б), 448. Вырезать из бумаги два равных прямоугольных треугольника и составить из них: 1) равнобедренный треугольник; 2) прямоугольник; 3) параллелограмм, не являющийся прямоугольником; 4) равновеликие фигуры |
||||