РЕШЕНИЕ ЗАДАЧ - Урок 2 - ЧЕТЫРЕХУГОЛЬНИКИ

Цель деятельности учителя

Создать условия для закрепления теоретического материала по теме “Прямоугольник. Ромб. Квадрат”, совершенствования навыков решения задач по данной теме, подготовки учащихся к контрольной работе

Термины и понятия

Ромб, квадрат, диагонали, углы

Планируемые результаты

Предметные умения

Универсальные учебные действия

У меют работать с геометрическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики

Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач.

Регулятивные: принимают и сохраняют учебные задачи.

Коммуникативные: умеют находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов.

Личностные: проявляют способность к эмоциональному восприятию математических объктов, задач, решений, рассуждений

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные

ресурсы

• Учебник.

• Задания для математического диктанта, самостоятельной работы

I этап. Актуализация опорных знаний

Математический диктант

Цель деятельности

Задания для самостоятельной работы

Проверить уровень теоретической подготовки

(И) После проведения диктанта осуществляется взаимопроверка.

1. Является ли прямоугольником параллелограмм, у которого есть прямой угол? (Да.)

2. Обязательно ли является прямоугольником четырехугольник, у которого есть прямой угол? (Нет.)

3. Верно ли, что каждый прямоугольник является параллелограммом? (Да.)

4. Верно ли, что каждый параллелограмм является прямоугольником? (Нет.)

5. Диагонали прямоугольника АЕКМпересекаются в точке О. Отрезок АО = 3. Найдите длину диагонали ЕМ. (6.)

6. Диагонали параллелограмма равны 3 и 5 дм. Является ли этот параллелограмм прямоугольником? (Нет.)

7. Диагонали четырехугольника равны. Обязательно ли этот четырехугольник прямоугольник? (Нет.)

8. Сумма длин диагоналей прямоугольника 13 см. Найдите длину каждой диагонали. (6,5.)

9. Периметр ромба равен 12 см. Найдите длины его сторон. (3 см.)

10. Верно ли, что каждый ромб является параллелограммом? (Да.)

11. Верно ли, что каждый параллелограмм является ромбом? (Нет.)

12. Ромб ABCD имеет прямой угол. Является ли этот ромб квадратом? (Да.)

13. Две соседние стороны параллелограмма равны и образуют прямой угол. Как называется такой параллелограмм? (Квадрат.)

14. Диагонали квадрата делят его на четыре треугольника. Найдите углы каждого треугольника. (45°.)

II этап. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

Выработать умение применять теоретические знания при решении задач

(Г) 1. Решение задач № 428, 434, 438.

2. Защита решений

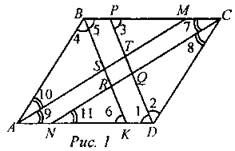
№ 428.

Решение:

1) DP - биссектриса => ∠1 = ∠2.

2) ∠1 = ∠3, как внутренние накрест лежащие при ВС || AD и секущей PD. Имеем ∠1 = ∠2 = ∠3.

3) Аналогично для биссектрисы угла В имеем ∠4 = ∠5 = ∠6.

4) Но ∠ABC = ∠ADC, поэтому ∠1 = ∠2 = ∠3 = ∠4 = ∠5 = ∠6.

∠5 и ∠3 соответственные при прямых PD и ВК и секущей ВС => PD|| ВК.

5) Аналогично доказывается, что AM || NC.

6) STQR - параллелограмм по определению.

7) ∆PCD - равнобедренный, так как ∠3 = ∠2, CQ — биссектриса и высота.

8) В параллелограмме STQR один угол прямой => он является прямоугольником.

№ 434.

Дано: ABCD - ромб, АС ∩ BD = О.

Доказать: ON = ОМ = ОЕ = OF.

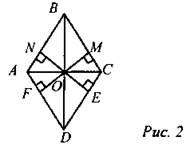
Доказательство:

1) Рассмотрим ∆BON и ∆ВОМ: ВО - общая, ∠NBO = ∠MBO (свойство ромба), следовательно, ∆BON = ∆ВОМ (по гипотенузе и острому углу).

Отсюда ОМ = ON (по определению равенства треугольников).

2) Аналогично через ∆FOD = ∆EOD имеем ОЕ = OF.

3) Рассмотрим ∆AOF и ∆СОМ: АО = ОС (свойство ромба), ∠OAF =∠OCM (свойство ромба), следовательно, ∆AOF = ∆СОМ (по гипотенузе и острому углу), следовательно, OF = ОМ (по определению равенства треугольников).

4. Вывод: ОМ = ON (из п. 1), ОЕ = OF (из п. 2), OF = ОМ (из п. 3), следовательно, ON = ОМ = ОЕ = OF.

№ 438.

Дано: ABCD - трапеция, АС ⊥ CD, ∠BAC = ∠CAD,

P_ABCD = 20 см, ∠D = 60°.

Найти: AD.

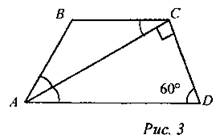
Решение:

1) Рассмотрим ∆ACD: ∠C = 90°, ∠D = 60°, следовательно, ∠А = 30°, значит, CD = 1/2AD.

2) Так как ∠ВАС = ∠CAD = 30°, значит, ABCD - равнобедренная трапеция, CD = АВ.

3) Так как ∠CAD = ∠BAC, следовательно, ∠ВАС = ∠BCA,следовательно, ∆АВС - равнобедренный, АВ = ВС.

4) Р_ABCD = АВ + ВС + CD + AD.

Так как CD = 1/2AD, а АВ = ВС = CD, то:

20 = 2,5AD; AD = 20 : 2,5; AD = 8 (см).

Ответ: 8 см

III этап. Самостоятельная работа

Цель деятельности

Задания для самостоятельной работы

Закрепить теоретические знания и практические умения при решении задач

(И)

Вариант I

1. Через точку пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны AD и ВС соответственно в точках E и F. Найдите стороны параллелограмма, если его периметр равен 28 см, АЕ = 5 см, BF = 3 см.

Ответ: 6 и 8 см.

2. Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10 см и 6 см, а один из углов равен 45°.

Ответ: 4 см.

3. Разделите данный отрезок на 5 равных частей (длину отрезка учитель определяет сам).

Вариант II

1. Биссектрисы углов А и D параллелограмма ABCD пересекаются в точке М, лежащей на стороне ВС. Найдите стороны параллелограмма, если его периметр равен 36 см.

Ответ: 6 и 12 см.

2. Найдите боковую сторону равнобедренной трапеции, основания которой равны 12 см и 6 см, а один из углов равен 120°.

Ответ: 6 см.

3. Разделите данный отрезок на 6 равных частей (длину отрезка учитель определяет сам)

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Какой этап урока был для вас самым сложным? Почему?

- Оцените свою работу.

- Какие вопросы у вас еще остались?

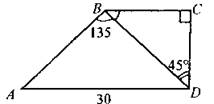
(И) Домашнее задание: подготовиться к контрольной работе.

Решить задачи.

1. В ромбе ABCD ∠D = 140°. Определите углы треугольника AOD (О - точка пересечения диагоналей).

2. На диагонали МР прямоугольника MNPQ отложены равные отрезки МА и РВ. Докажите, что ANBQ - параллелограмм.

3. Найти ВС.