ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ

ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ. ТЕМА № 1

Четырехугольники

1. Диагонали параллелограмма АВС К равны 5 см и 8 см, сторона ВС равна б см. Найдите периметр треугольника АКО, где О — точка пересечения диагоналей.

2. Диагональ АС параллелограмма ABCD образует с его сторонами АВ и AD углы, равные 46° и 31°. Найдите углы треугольника АВС.

3. Периметр параллелограмма равен 40 см. Найдите стороны параллелограмма, если одна из них: 1) в 4 раза меньше другой; 2) на 7 см больше другой.

4. В треугольнике МРК на продолжении медианы ME за точку Е отложен отрезок ED, равный ME. Докажите, что MPDK — параллелограмм.

5. Докажите, что диагональ параллелограмма разбивает его на два равных треугольника.

6. В параллелограмме ABCD на сторонах ВС и AD взяты соответственно точки Н и P — середины этих сторон. Известно, что АВ = 7 см, ВС = 9 см. Определите вид четырехугольника АВНР (ответ обоснуйте) и найдите его периметр.

7. Диагонали прямоугольника КМОР пересекаются в точке А, сторона МО равна 7 см, диагональ МР равна 9 см. Определите вид треугольника КРА (ответ обоснуйте) и найдите его периметр.

8. В прямоугольнике ABCD биссектриса угла А пересекает сторону ВС в точке К. Докажите, что треугольник АВК — равнобедренный.

9. В прямоугольнике ABCD диагональ АС делит угол BAD в отношении 4:5. Найдите углы треугольника COD (О — точка пересечения диагоналей).

10. Диагонали ромба разбивают его на четыре треугольника. Найдите углы этих треугольников, если один из углов ромба 160°.

11. Одна из диагоналей ромба равна его стороне. Определите углы ромба.

12. Найдите стороны ромба, если его периметр равен 44.

13. Докажите, что диагонали квадрата разбивают его на четыре равных равнобедренных прямоугольных треугольника.

14. Докажите, что если диагонали трапеции равны, то она равнобедренная.

15. В трапеции ОВСК с основаниями ВС и ОК диагонали пересекаются в точке М. Найдите углы треугольника МОК, если ∠KBC = 41°, ∠OCB = 34°.

16. В равнобедренной трапеции ABCD отрезок СМ параллелен боковой стороне АВ (М ∈ AD). Известно, что AD = 30 см, ВС = 22 см, АВ = 17 см.

1) Определите вид четырехугольника АВСМ.

2) Определите вид треугольника MCD и найдите его периметр.

17. В трапеции АРОВ ∠A = 51°, ∠B = 90°. Прямая, параллельная стороне АР, проходит через вершину О и точку D на большем основании АВ. Найдите острые углы треугольника ODB.

18. В трапеции МРКО (МО - большее основание) диагональ МК является биссектрисой угла М. Найдите величину угла МКО, если ∠KPM = 140° и МК = КО.

19. В равнобедренной трапеции диагонали являются биссектрисами ее тупых углов. Найдите периметр трапеции, если длины оснований равны 5 см и 8 см.

20. Через точку пересечения диагоналей параллелограмма проведены прямые, параллельные его сторонам. Найдите периметры полученных параллелограммов, если периметр данного параллелограмма равен 32 м.

Укажите, какие высказывания (№ 21—41) верны, какие неверны.

Параллелограмм

21. Четырехугольник, у которого две стороны параллельны, а две другие равны, — параллелограмм.

22. Четырехугольник, у которого сумма противоположных углов равна 180°, — параллелограмм.

23. Биссектрисы углов параллелограмма, не являющегося ромбом, пересекаясь, образуют прямоугольник.

24. Сумма расстояний от любой точки, лежащей внутри параллелограмма, до всех его сторон - величина постоянная.

25. Существует параллелограмм, у которого диагональ равняется его стороне.

26. Из вершин тупых углов параллелограмма проведены высоты. Концы этих четырех высот являются вершинами параллелограмма.

27. Существует параллелограмм, одна сторона которого равна 5, а его диагонали равны 4 и 6.

28. Существует параллелограмм, одна сторона которого равна 5, а его диагонали равны 4 и 3.

29. Существует параллелограмм, одна сторона которого равна 5, а его диагонали равны 7 и 6.

30. Если в четырехугольнике два угла прямые, то он является прямоугольником.

31. Параллелограмм, у которого есть прямой угол, является прямоугольником.

32. Четырехугольник, у которого есть прямой угол, является прямоугольником.

33. Существует прямоугольник, в котором есть точка, одинаково удаленная от всех его сторон.

34. Существует в прямоугольнике точка, одинаково удаленная от всех его вершин.

35. Существует ромб, диагональ которого в два раза больше его стороны.

36. Неравные ромбы могут иметь равные периметры.

37. Существует ромб, в котором сторона равна его высоте.

38. Если сумма внешних углов при каждой стороне четырехугольника равна 180°, то четырехугольник является параллелограммом.

39. Существует треугольник, у которого углы равны трем углам какого-нибудь параллелограмма.

40. Параллелограмм, у которого диагонали равны, является прямоугольником.

Трапеция

41. Существует трапеция, в которой диагональ является биссектрисой ее угла.

42. Биссектриса угла параллелограмма делит сторону параллелограмма на отрезки 9 см и 10 см. Найдите периметр параллелограмма.

Симметрии

43. Начертите прямоугольный треугольник АВС (угол С — прямой). Постройте симметричный ему треугольник относительно вершин С и А.

44. Начертите треугольник АВС. Постройте симметричный ему треугольник относительно сторон АВ и ВС.

45. Дан равнобедренный тупоугольный треугольник МКС с основанием СК. Постройте точку Р, симметричную точке М относительно прямой СК. Определите вид четырехугольника КМСР.

46. Дан равнобедренный тупоугольный треугольник МКС с основанием СК. Постройте отрезок АВ, симметричный СК, относительно вершины М. Определите вид четырехугольника САВК.

47. Постройте фигуру, симметричную ромбу относительно точки пересечения диагоналей.

48. Постройте фигуру, симметричную равностороннему треугольнику относительно точки пересечения высот.

49. Постройте фигуру, симметричную кругу относительно его центра.

50. Постройте центр симметрии данного параллелограмма, не используя его вершин.

51. Внутри острого угла А дана точка М. Постройте треугольник МРК наименьшего периметра вершины Р и К на сторонах угла А.

52. Через данную точку проведите прямую, которая пересекает две данные прямые под равными углами.

ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ. ТЕМА № 2

Площадь. Теорема Пифагора

1. Треугольник АВС — равнобедренный с основанием АС. Найдите боковые стороны, если высота ВН равна 8 см, основание 12 см.

2. Треугольник АВС — равнобедренный с основанием АС. Найдите основание, если медиана ВМ равна 12 см, а боковая сторона 13 см.

3. В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна 6,5 см, длина одного катета — 5 см. Найдите длину другого катета.

4. Найдите высоту, проведенную к основанию равнобедренного треугольника с боковой стороной 10 см и основанием 12 см.

5. Сторона ромба равна 20 см, а одна из его диагоналей равна 24 см. Найдите длину второй диагонали.

6. В окружности с радиусом 5 см проведена хорда, равная 6 см. Найдите длину отрезка, соединяющего центр окружности с серединой хорды.

7. Найдите периметр параллелограмма, изображенного на рисунке, если АН = 9 см, ВН = 12 см, ВК = 20 см.

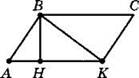
8. Боковая сторона равнобедренной трапеции равна 17 см, меньшее основание — 11 см, высота — 15 см. Найдите большее основание.

9. Основания трапеции равны 4 см и 8 см. Углы при большем основании равны 30° и 60°. Найдите длины боковых сторон трапеции.

10. Основания трапеции равны 6 см и 11 см, боковые стороны равны 3 см и 4 см. Найдите длину отрезка, соединяющего середины оснований.

11. В трапеции высота равна 12 дм, диагонали равны 15 дм и 20 дм. Найдите площадь трапеции.

12. Найдите диагональ квадрата со стороной 12 см.

13. Найдите высоту равностороннего треугольника, если его сторона равна 8 см.

14. В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна 6,5 см, длина одного катета равна 5 см. Найдите площадь треугольника.

15. Найдите сторону квадрата, если его диагональ равна 4 см.

16. К прямой а проведены наклонные АВ = 17 см, АС = 10 см и перпендикуляр AD = 8 см. Найдите: 1) BD; 2) CD; 3) ВС.

17. Определите площадь прямоугольника, если одна из его сторон равна 8 см, а диагональ равна 10 см.

18. Чему равна площадь равнобедренного треугольника с основанием 20 см и боковой стороной 26 см?

19. Определите площадь параллелограмма ABCD, если: ВС = 6 см, CD = 10 см, ∠ABC = 120°.

20. Найдите площадь параллелограмма ABCD, если АВ = 15 см, ВК = 9 см, DK = 10 см, где точка К лежит на стороне AD и ВК ⊥ AD.

21. В трапеции ABCD (AD — большее основание) проведены высоты ВК и СМ. Найдите площадь трапеции, если АВ = 10, АК = 6, КМ = 4, DM = 8.

22. Найдите площадь ромба с диагоналями 5 см и 13 см.

23. Найдите площадь равностороннего треугольника, если его сторона равна 12 см.

24. Площадь параллелограмма равна 30 см². Найдите его периметр, если высоты параллелограмма равны 5 см и 3 см.

25. Точки А и Б — середины сторон МР и МО параллелограмма МРКО. Прямые ОА и РВ пересекаются в точке С. Найдите площади четырехугольника MACВ и треугольника АВС, если площадь параллелограмма равна 36 см².

26. Укажите, высказывание верное или неверное:

Медиана треугольника разбивает его на два равновеликих треугольника.

27. В треугольнике АВС стороны ВС = 4 и АС = 5, а сумма длин высот, проведенных к этим сторонам, равна третьей высоте. Найдите длину АВ.

28. Две стороны треугольника равны 6 и 8. Медианы, проведенные к ним, перпендикулярны. Найдите третью сторону.

29. Периметр ромба равен 4 м, длины его диагоналей относятся как 3:4. Найдите площадь ромба.

30. В трапеции, площадь которой равна 110 м², высота 11 м, а разность длин оснований равна 6 м, найдите длины оснований.

31. Вычислите площадь прямоугольной трапеции, если ее острый угол равен 60°, меньшее основание равно 7 см, а большая боковая сторона равна 10 см.

32. Диагональ равнобедренной трапеции делит ее тупой угол пополам. Меньшее основание трапеции равно 3 см, периметр равен 42 см. Найдите площадь трапеции.

33. Одна из сторон треугольника на 5 см меньше другой, высота делит третью сторону на отрезки длиной 9 см и 16 см. Найдите периметр треугольника.

34. В равнобедренном треугольнике высоты, проведенные к основанию и боковой стороне, равны соответственно 5 см и б см. Найдите длину боковой стороны.

35. В параллелограмме АВСК проведен перпендикуляр ВН к стороне АK, при этом точка Н лежит на стороне АК. Найдите площадь параллелограмма, если известно, что АН = 8 см, НК = 10 см, угол АВН равен 30°.

ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ. ТЕМА № 3

Подобие треугольников. Решение прямоугольных треугольников

1. Даны две параллельные прямые а и b. Через точку М, лежащую между этими прямыми, проведены секущие НК и OP (Н ∈ а, К ∈ b, О ∈ а, Р ∈ b).

1) Докажите, что

2) Найдите РК, если ОН = 14, МН = 12, МК = 18.

3) Найдите ОР и НК, если ОН = 10, РК = 15, ОМ = 6, МК = 9.

2. Дана трапеция КМРО (МР — меньшее основание). Боковые стороны продолжены до пересечения в точке D.

1) Укажите полученные при этом подобные треугольники. Докажите их подобие.

2) Найдите большее основание, если МР = a, DM = b, МК = с.

3) Найдите боковые стороны трапеции, если МР = 12 см, КО = 28 см, DK = 35 см, DP = 21 см.

3. В прямоугольном треугольнике АВС проведен отрезок DE, причем DE ⊥ АВ (см. рисунок). Укажите имеющиеся на рисунке подобные треугольники. Запишите пропорциональность их соответствующих сторон.

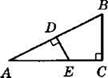
4. В остроугольном треугольнике МВК проведены высоты МР и КС, пересекающиеся в точке D. Докажите, что:

5. Докажите, что высоты подобных треугольников относятся как соответствующие стороны.

6. В треугольнике МРК проведены средние линии CD и СЕ (С ∈ РК, D ∈ МК, E ∈ РМ).

1) Определите вид четырехугольника MECD.

2) Найдите его периметр, если АМРК — равносторонний со стороной а.

3) Найдите периметр треугольника DCK, если МР = 8 см, МК = 7 см, РК = 6 см.

7. В треугольнике АВС проведены медианы АЕ и BD. Найдите периметр треугольника АВС, если периметр треугольника DCE равен р.

8. Треугольник МКР — равнобедренный с основанием МР.

1) Найдите основание, если высота КО равна 8 см, ∠MKP = 120°.

2) Найдите боковую сторону, если медиана KL равна 10 см, ∠M = 34°.

3) Найдите основание, если боковая сторона равна б см, ∠MKP = 96°.

9. Высота AM треугольника АВС делит сторону ВС на отрезки ВМ и МС. Найдите стороны треугольника, если AM = 3 см, ∠B = 45°, ∠C = 60°.

10. Угол между радиусами ОА и ОB окружности равен 110°. Чему равна хорда АВ, если радиус окружности равен 4 см?

11. Найдите площадь равнобедренного треугольника, если высота, проведенная к основанию, равна h, а угол между этой высотой и боковой стороной равен 60°.

12. В треугольнике АВС со сторонами АВ = 6, АС = 7, ВС = 8 на АВ взята точка М и проведена прямая МК (К е ВС) у параллельная стороне АС, так, что AM = ВК. Найдите длину МК.

13. Через точку М, принадлежащую стороне АС треугольника АВС, проведены прямые МК (К ∈ ВА) и МР (Р ∈ ВС), параллельные соответственно сторонам СВ и АВ треугольника АВС. Найдите площадь треугольника КВР, если площади треугольников АКМ и МРС равны соответственно 12 и 48.

14. Известно, что в трапеции ABCD (ВС и AD — основания) площади треугольников AOD и BОС равны соответственно 16 и 9 (О — точка пересечения диагоналей). Найдите площадь трапеции.

15. Площадь одного квадрата в 16 раз больше площади другого. Во сколько раз диагональ первого квадрата больше диагонали второго квадрата?

16. Через середину М стороны ВС параллелограмма ABCD, площадь которого равна 6, и вершину А проведена прямая, пересекающая диагональ BD в точке О. Найдите площадь четырехугольника OMCD.

17. Сходственные стороны подобных треугольников равны 2 см и 7 см, площадь первого треугольника равна 12 см². Найдите площадь второго треугольника.

18. В ромбе угол равен 60°, диагональ, проведенная из вершины этого угла, равна 6√3 см. Найдите периметр, площадь и высоту ромба.

19. Длины оснований трапеции m и n. Прямая, проходящая через точку пересечения диагоналей трапеции параллельно основаниям, пересекает боковые стороны в точках М и N. Найдите длину отрезка MN.

20. Укажите, верно ли высказывание?

Любые равносторонние треугольники подобны.

21. Боковая сторона равнобедренного треугольника АВС равна 15, а его площадь равна 67,5. Проведены высоты BE и АН, пересекающиеся в точке О. Найдите площадь треугольника ВОН.

22. Отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника, перпендикулярны и равны 24 см и 10 см. Определите вид четырехугольника с вершинами в серединах сторон данного четырехугольника и найдите его периметр.

23. Определите вид четырехугольника, вершинами которого являются середины сторон выпуклого четырехугольника, если известно, что отрезки, соединяющие середины противоположных сторон четырехугольника, равны.

24. Середины сторон равнобедренной трапеции попарно соединены. Определите вид получившегося четырехугольника.

25. Найдите площадь прямоугольного треугольника, если известно, что один из катетов равен 15 дм и высота, проведенная к гипотенузе, равна 12 дм.

26. Точка на гипотенузе прямоугольного треугольника, равноудаленная от обоих катетов, делит гипотенузу на отрезки длиной 30 см и 40 см. Найдите катеты треугольника.

27. В прямоугольном треугольнике биссектриса острого угла делит противоположный катет на отрезки длиной 4 см и 5 см. Найдите площадь треугольника.

28. Площадь треугольника АВС равна 15 м². На стороне АС взята точка К так, что АК : КС = 2 : 3. Длина перпендикуляра КН, проведенного на сторону ВС, равна 6 м. Найдите длину ВС.

ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ. ТЕМА № 4

Окружность

1. Из точки М, лежащей вне окружности, проведены касательные МА и МВ (А и В — точки касания). Докажите, что МА = МВ.

2. К окружности с центром О проведена касательная АС (С — точка касания). Найдите радиус окружности, если ОА = 6 см, АС = 2√5 СМ.

3. Прямые АВ и АС касаются окружности с центром О радиусом 8 см, B и С — точки касания. Найдите отрезки АВ и АС, если: 1) ∠BAC = 60°; 2) ∠BAC = 48°.

4. Дан квадрат со стороной 7 см. Найдите радиусы вписанной и описанной окружностей.

5. Найдите радиусы вписанной и описанной окружностей равностороннего треугольника со стороной 2 м.

6. Определите площадь прямоугольника, если одна из сторон равна 8 см, а радиус описанной около него окружности равен 8,5 см.

7. В окружности проведены хорда СР и диаметр АВ (см. рисунок). Найдите:

1) углы треугольника АВС, если ∠P = α;

2) радиус окружности, если РМ = 6, СМ = 8, ВМ = 4.

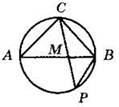
8. В треугольнике АВС известны стороны АВ = 5, ВС = 6, АС = 7. Окружность, вписанная в треугольник, касается его сторон АВ, ВС, АС соответственно в точках К, М, Р. Найдите длины отрезков АК, ВМ, СР.

9. Дан треугольник АВС. Окружность, проходящая через точки А и С, пересекает стороны ВА и ВС соответственно в точках К и М. Найдите подобные треугольники и докажите их подобие.

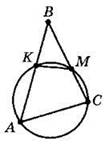
10. Радиус окружности пересекает хорду в точке А. Докажите, что радиус перпендикулярен хорде, если точка А — ее середина.

11. Радиус окружности пересекает хорду в точке А. Докажите, что точка А — середина хорды, если радиус перпендикулярен хорде.

12. Из центра окружности к хорде АВ проведен перпендикуляр ОМ, равный 8 см. Найдите радиус окружности, если ∠ABO = 30°.

13. Из центра О окружности к хорде АВ проведен перпендикуляр ОМ, равный 8 см. Найдите хорду АВ, если ∠BOM 45°.

14. Из точек А и В, лежащих вне окружности на одинаковом расстоянии от центра, проведены касательные AD и ВС (D и С — точки касания). Докажите, что отрезки AD и ВС равны.

15. Через точки М и К, лежащие на окружности с центром О, проведены касательные MN и KN. Докажите, что ΔMON = ΔKON.

16. Через точки М и К, лежащие на окружности с центром О, проведены касательные MN и KN. Докажите, что NO — биссектриса угла MNK.

17. Докажите, что если РК и RS — диаметры одной окружности, то хорды RK и PS параллельны.

18. Даны две окружности с общим центром; АС — диаметр одной окружности, a BD — диаметр другой окружности. Докажите, что отрезки AD и ВС равны и параллельны.

19. В окружности с центром К проведены хорды АВ и CD. Докажите, что эти хорды равны, если ∠KAB = ∠KCD.

20. Докажите, что у равнобедренного треугольника центры вписанной и описанной окружностей лежат на прямой, которая проходит через медиану, проведенную к основанию.

21. В треугольник АВС вписана окружность с центром О. Найдите углы треугольников АОВ, ВОС и АОС, если ∠BAC = 40°, ∠ABC = 60°.

22. Окружность, вписанная в равнобедренный треугольник DEF, касается основания DE в точке А, а боковых сторон в точках В и С. Докажите, что периметры треугольников ABF и ACF равны.

23. Окружность, вписанная в равнобедренный треугольник DEF, касается основания DE в точке А, а боковых сторон в точках Б и С. Найдите отрезки BF и CF, если периметр треугольника DEFравен 28 см, а основание равно 10 см.

24. Периметр прямоугольного треугольника равен 60 см, а гипотенуза равна 26 см. Найдите: 1) площадь треугольника; 2) радиусы вписанной в треугольник и описанной около треугольника окружностей.

25. В прямоугольный треугольник с площадью 24 см² вписана окружность. Точка касания с окружностью делит гипотенузу в отношении 2 : 3. Найдите длины сторон треугольника.

26. Найдите радиус окружности, описанной около прямоугольного треугольника, если радиус окружности, вписанной в этот треугольник, равен 3 см, а один из катетов равен 10 см.

27. В ромб, который делится своей диагональю на два равносторонних треугольника, вписана окружность радиуса 2. Найдите сторону ромба.

28. В выпуклом четырехугольнике ABCD углы ABD и ACD равны. Найдите величину угла BАD, если углы DBC и CDB равны соответственно 47° и 73°.

29. В прямоугольном треугольнике АBС (угол С — прямой) проведена высота СН. В каждый из треугольников АСН и ВСН вписана окружность. Найдите квадрат расстояния между центрами этих окружностей, если АС = 12, ВС = 5.

30. Окружность с центром в точке О касается сторон угла А в точках B и С. Прямая ВО пересекает луч АС в точке К. Найдите длину отрезка АО, если АС = 8 см, СК = 2 см.

31. Окружность с центром в точке О касается сторон угла А в точках B и С. Прямая ВО пересекает луч АС в точке К. Найдите длину отрезка АK, если АО = 3√5 см, а радиус окружности равен 3 см.

ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ. ТЕМА № 5

Средняя линия трапеции

1. Верно ли, что в трапеции средняя линия проходит через точку пересечения диагоналей?

2. Основания трапеции равны тип. Найдите длину отрезка, соединяющего середины диагоналей трапеции.

3. В равнобедренной трапеции биссектриса тупого угла делит основание пополам. Высота трапеции равна 5 см, а средняя линия - 14 см. Найдите периметр трапеции.

4. Высоты равнобедренной трапеции делят ее на квадрат и два равнобедренных треугольника, а ее боковая сторона равна 6√2 см. Найдите среднюю линию.

5. В равнобедренной трапеции средняя линия равна 12 см, высота - 5 см. Найдите диагональ трапеции.

6. В прямоугольной трапеции ABCD (AD - большее основание) диагональ АС является биссектрисой угла А и перпендикулярна боковой стороне CD. Найдите длину средней линии трапеции, если АС = 7√2.

7. Прямая, параллельная боковой стороне трапеции, отсекает от нее ромб. Площади полученных фигур относятся как 4 : 5. Найдите отношение стороны ромба к средней линии трапеции.

8. Средняя линия трапеции разбивает ее на две трапеции, площади которых относятся как m : n. Найдите отношение оснований трапеции.

9. Диагонали трапеции равны 10 см и 24 см, а средняя линия равна 13 см. Найдите площадь трапеции.