ПРОВЕРОЧНЫЕ РАБОТЫ

ПРОВЕРОЧНАЯ РАБОТА № 1. Параллелограмм. (1)

ВАРИАНТ 1

1. В параллелограмме ABCD сторона CD равна 3 см, диагонали равны 7 см и 4 см, О — точка пересечения диагоналей. Чему равен периметр треугольника AOB?

2. В параллелограмме один угол равен 44°. Найдите остальные углы параллелограмма.

3*. В треугольнике АВС ∠А = 50°. Из точки, взятой на стороне ВС, проведены две прямые, параллельные сторонам АВ и АС. Определите вид получившегося четырехугольника и все его углы.

ВАРИАНТ 2

1. В параллелограмме ABCD диагонали равны 8 см и 5 см, сторона ВС равна 3 см, О — точка пересечения диагоналей. Чему равен периметр треугольника AOD?

2. В параллелограмме один из углов равен 144°. Найдите остальные углы параллелограмма.

3*. Из точки, взятой на одной из сторон равностороннего треугольника, проведены две прямые, параллельные другим его сторонам. Определите вид получившегося четырехугольника и все его углы.

ВАРИАНТ 3

1. Периметр параллелограмма равен 16 см. Чему равны стороны параллелограмма, если известно, что одна его сторона в 3 раза больше другой?

2. В ромбе ABCD ∠D = 140°. Определите углы треугольника AOD (О — точка пересечения диагоналей).

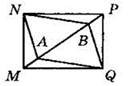
3*. На диагонали МР прямоугольника MNPQ отложены равные отрезки МА и РВ (см. рисунок). Докажите, что ANBQ — параллелограмм.

ВАРИАНТ 4

1. Одна из сторон параллелограмма в 4 раза больше другой, а его периметр равен 30 см. Чему равны стороны параллелограмма?

2. В ромбе MNPQ ∠N = 100°. Определите углы треугольника MON (О — точка пересечения диагоналей).

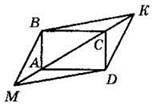
3*. На продолжении диагонали АС прямоугольника ABCD отложены равные отрезки AM и СК (см. рисунок). Докажите, что MBKD — параллелограмм.

ПРОВЕРОЧНАЯ РАБОТА № 2 . Параллелограмм. (2)

ВАРИАНТ 1

1. Известно, что четырехугольник MNPK является параллелограммом. Докажите, что ΔMNK = ΔPKN.

2. Диагонали квадрата CDEF пересекаются в точке О. Чему равны углы треугольника DOC?

3*. Начертите произвольный треугольник DEF, на стороне DE отметьте точку А, не являющуюся ее серединой. Постройте фигуру, симметричную треугольнику DEF относительно точки А.

4*. Определите вид четырехугольника DANB и найдите его периметр (см. рисунок), если MN = NK = 26 см, AD || NK, DB || MN и MD = DK.

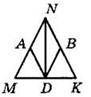
ВАРИАНТ 2

1. В параллелограмме КМ NO диагонали пересекаются в точке D. Докажите, что ΔKDM = ΔNDO.

2. Диагонали ромба ABCD пересекаются в точке О. Найдите углы АОВ и ВАО, если ∠BAD = 44°.

3*. Начертите прямоугольник МРОК. Постройте фигуру” симметричную ему относительно диагонали ОМ.

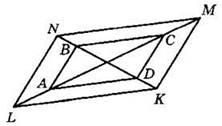
4*. Четырехугольник ABCD — параллелограмм, отрезки AL, BN, СМ и DK равны (см. рисунок). Докажите, что LNMK также является параллелограммом.

ВАРИАНТ 3

1. Известно, что четырехугольник ABCD является ромбом. Докажите, что ΔАВС = ΔADC.

2. Диагонали прямоугольника BCDE пересекаются в точке О, диагональ BD равна 32 м. Найдите длины отрезков ОЕ и ОС.

3*. Начертите прямоугольный треугольник АВС, на гипотенузе АВ отметьте точку А, не являющуюся ее серединой. Постройте фигуру, симметричную треугольнику АВС относительно точки N.

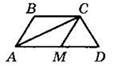
4*. В трапеции ABCD (см. рисунок) АС — биссектриса угла ВАМ, СА — биссектриса угла ВСМ, ВС = 16 см. Определите вид четырехугольника АВСМ и найдите его периметр.

ВАРИАНТ 4

1. Четырехугольник КМРО — квадрат. Чему равны углы треугольника МОР?

2. Диагонали прямоугольника BCDE пересекаются в точке К. Докажите, что ΔВСК = ΔDEK.

3*. Начертите параллелограмм MNPR. Постройте фигуру, симметричную ему относительно диагонали РМ.

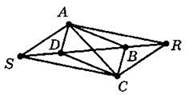
4*. Диагональ DB параллелограмма ABCD продолжена на равные отрезки BR и DS (см. рисунок). Докажите, что RASC также является параллелограммом.

ПРОВЕРОЧНАЯ РАБОТА № 3 . Теорема Пифагора

ВАРИАНТ 1

1. Найдите сторону ромба, если его диагонали равны 12 см и 16 см.

2. В параллелограмме МРОК высота PH делит сторону МК на отрезки МН = 9 м и НК = 8 м. Найдите площадь параллелограмма, если сторона МР равна 15 м.

3*. Найдите катеты прямоугольного треугольника, если один из них в 2 раза больше другого, а гипотенуза равна 5 см.

4*. В ромбе ABCD высота ВК делит сторону AD на отрезки АK = 12 см и KD = 8 см. Найдите диагональ BD и высоту ВК.

ВАРИАНТ 2

1. Найдите боковую сторону равнобедренного треугольника BCD, если основание BD равно 10 см, а высота СК равна 12 см.

2. В параллелограмме МРОК диагональ РК перпендикулярна стороне МК. Найдите его площадь, если сторона МР равна 10 м, а сторона МК равна 8 м.

3*. Найдите стороны прямоугольника, если одна из них в 3 раза меньше другой, а диагональ прямоугольника равна 20 м.

4*. В равнобедренном треугольнике АВС высота AD разбивает боковую сторону ВС на отрезки BD = 24 см и DC = 1 см. Найдите основание АС и высоту AD.

ВАРИАНТ 3

1. Найдите высоту CN равнобедренного треугольника АВС, если его основание АВ равно 18 см, а боковая сторона равна 15 см.

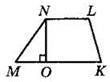
2. Отрезок NO — высота трапеции MNLK (см. рисунок). Найдите площадь трапеции, если MN = 10 см, МО = 6 см, ОК = 12 см, NL = 8 см.

3*. Найдите катет прямоугольного треугольника, если он в 2 раза меньше гипотенузы, а второй катет равен 6 м.

4*. В равнобедренной трапеции ABCD большое основание AD равно диагонали. Высота ВМ разбивает основание AD на отрезки AM = 6 см и MD = 9 см. Найдите боковую сторону и высоту.

ВАРИАНТ 4

1. Найдите основание BD равнобедренного треугольника BAD, если его боковая сторона равна 20 см, а высота AM равна 15 см.

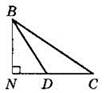
2. Найдите площадь треугольника BCD (см. рисунок), если CD = 12 см, DN = 6 см, BD = 10 см.

3*. Одна из сторон прямоугольника равна 8 м. Чему равна смежная сторона, если она в 3 раза меньше диагонали?

4*. Диагонали прямоугольника ABCD пересекаются в точке О. Перпендикуляр AM, опущенный на диагональ BD, разбивает отрезок ОВ на части: ОМ = 24 см и ВМ = 1 см. Чему равны перпендикуляр AM и сторона АВ?

ПРОВЕРОЧНАЯ РАБОТА № 4. Подобие треугольников

ВАРИАНТ 1

1. Определите стороны прямоугольника ABCD, если BD = 12, ∠ADB = β.

2. Прямые а и b параллельны (см. рисунок).

1) Докажите, что

2) Найдите ОК, если ОВ = 20, ВР = 12, МР = 15.

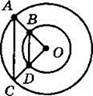
3*. Точка О — общий центр двух окружностей (см. рисунок). Докажите, что треугольники АОС и BOD подобны.

4*. На сторонах треугольника АВС взяты точки М ∈ АВ и К ∈ АС. Найдите сторону АС, если МК || ВС, КС = 5, МК = 12, ВС = 15.

ВАРИАНТ 2

1. Определите катеты прямоугольного треугольника МОК, если его гипотенуза МК равна 16, ∠M = γ.

2. В трапеции КМОР основания МО и КР равны 12 см и 16 см соответственно, а ее диагонали пересекаются в точке D. Найдите длину отрезка DO, если KD = 20 см.

3*. Докажите, что треугольники АОВ и DOC подобны, если О — общий центр двух окружностей (см. рисунок).

4*. В прямоугольном треугольнике BCD из точки М, лежащей на гипотенузе ВС, опущен перпендикуляр MN на катет BD. Найдите гипотенузу, если MN = 12 см, CD = 18 см, МС = 8 см.

ВАРИАНТ 3

1. Определите стороны прямоугольника ABDE, если известно, что AD = 16, ∠DAE = а.

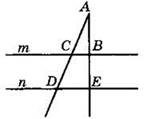
2. Прямые m и n параллельны (см. рисунок).

1) Докажите, что

2) Найдите DE, если АВ = 15 см, ВС = 12 см, BE = 10 см.

3*. В треугольнике ABD проведены высоты AM и ВН (см. рисунок). Докажите, что треугольники АОН и ВОМ подобны.

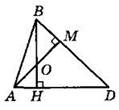
4*. Отрезки АВ и CD пересекаются в точке К, причем прямые АС и BD параллельны, АС = 16, DC = 39, KD = 27. Найдите длину отрезка BD.

ВАРИАНТ 4

1. Определите катеты прямоугольного треугольника РКН, если его гипотенуза РК равна 18, ∠P = β.

2. В трапеции BCDE основание CD равно 20 см, а ее диагонали пересекаются в точке А. Найдите основание BE, если АВ = 18 см, AD = 15 см.

3*. В треугольнике ADC проведены высоты AN и СК (см. рисунок). Докажите, что треугольники АОК и CON подобны.

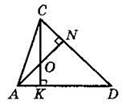
4*. В трапеции CDEF (CF — большее основание) боковые стороны продолжены до пересечения в точке Р. Найдите основание DE, если CF = 21, EF = 16, РЕ = 12.

ПРОВЕРОЧНАЯ РАБОТА № 5 . Окружность

ВАРИАНТ 1

1. Из точки С к окружности с центром О проведены касательные С А и CD, А и D — точки касания. Найдите углы треугольника АОС, если ∠ACD = 50°.

2. Прямоугольный треугольник с катетами 12 см и 16 см вписан в окружность. Найдите ее радиус.

3*. Хорды АВ и CD пересекаются в точке Е. Найдите длины отрезков АЕ и BE, если АВ = 17, СЕ = 12, DE = 6.

4*. Треугольник DBC — равнобедренный с основанием DC. Его периметр равен 34 см, сторона BD равна 10 см. Найдите длины отрезков DN и BN (N — точка касания вписанной окружности со стороной DB).

ВАРИАНТ 2

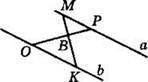
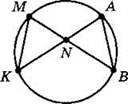
1. Найдите ∠B, если известно, что ∠M = 55°, ∠MNK = 60° (см. рисунок).

2. В окружности с радиусом 7,5 см проведены диаметр АС и хорда АК, равная 9 см. Найдите длину хорды СК.

3*. Хорда, равная 19 м, пересекается с другой хордой, точка пересечения делит вторую хорду на отрезки 6 м и 10 м. На какие отрезки разделилась первая хорда?

4*. Треугольник МРК — равнобедренный, его основание МК равно 16 м, а периметр равен 52 м. Найдите длины отрезков AM и АР (А — точка касания вписанной окружности со стороной МР).

ВАРИАНТ 3

1. Отрезки АВ и AD — касательные к окружности с центром О, точки В и D — точки касания. Найдите углы треугольника АВО, если ∠BAD = 56°.

2. В окружность с радиусом 10 см вписан прямоугольный треугольник, один катет которого равен 16 см. Найдите второй катет.

3*. Две хорды пересекаются в точке, которая делит одну из них на отрезки 8 м и 9 м. На какие отрезки разделилась вторая хорда, если она равна 22 м?

4*. Треугольник ABD — равнобедренный с основанием AD. Его периметр равен 64 см, DB = 20 см. Найдите длины отрезков DM и ВM (М — точка касания вписанной окружности со стороной BD).

ВАРИАНТ 4

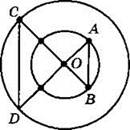
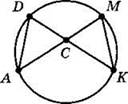
1. Найдите ∠K, если ∠D = 62°, ∠ACD = 88° (см. рисунок).

2. Две хорды MN и РК пересекаются в точке С. Найдите отрезки СР и СК, если РК = 17 см, МС = 4 см, CN = 15 см.

3*. В окружности проведены диаметр KN и хорды ВК = 8 см и BN = 6 см. Чему равен радиус окружности?

4*. Треугольник MRS — равнобедренный, его периметр равен 66 м, а основание MS равно 26 м. Найдите длины отрезков AM и AR (А — точка касания вписанной окружности со стороной MR).