Поурочные разработки по алгебре 7 класс - к учебнику Ю.Н. Макарычева - 2014 год
Разложение на множители суммы и разности кубов - РАЗНОСТЬ КВАДРАТОВ. СУММА И РАЗНОСТЬ КУБОВ - ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
Цель: рассмотреть формулы суммы и разности кубов.
Планируемые результаты: научиться раскладывать выражения на множители с помощью формул суммы и разности кубов.
Тип уроков: урок-исследование, урок-практикум.
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Найдите значение выражения:
![]()
2. Разложите на множители многочлен:
![]()
3. Решите уравнение ![]()
Вариант 2
1. Найдите значение выражения:
![]()
2. Разложите на множители многочлен:
![]()
3. Решите уравнение ![]()
III. Работа по теме уроков
Приведем еще две формулы сокращенного умножения.
![]()
Это тождество называют формулой суммы кубов. Заметим, что выражение а2 - ab + b2 называют неполным квадратом разности а и b (отличается от полного квадрата разности (а - b)2 = а2 - 2ab+ b2 тем, что вместо удвоенного произведения чисел а и b стоит просто их произведение).
В соответствии с формулой (1) сумма кубов двух чисел (выражений а и b) равна произведению суммы этих чисел (выражений а и b) и неполного квадрата их разности (а2 - ab + b2).
Выведем формулу (1) алгебраическим способом, преобразовав правую часть в левую.
Умножим два многочлена и получаем ![]()
![]()
Заметим, что формулу (1) можно получить и геометрическим способом, рассмотрев объемы параллелепипедов.
Формула разности кубов имеет аналогичный вид:
![]()
Разность кубов двух чисел (выражений а и b) равна произведению разности этих чисел (выражений а и b) и неполного квадрата их суммы (а2 + ab + b2).
Формулу (2) можно вывести аналогично формуле (1), умножив многочлены:
![]()
Формулу (2) можно получить непосредственно из формулы (1):
![]()
Пример 1
Докажем, что выражение 1233 + 273 кратно 150.
Используя формулу (1), получим ![]()
![]() Видно, что данное выражение без остатка делится на 150.
Видно, что данное выражение без остатка делится на 150.
Пример 2
Вычислим значение выражения ![]() без калькулятора.
без калькулятора.
Используя формулу (2) и формулу квадрата суммы, получаем
![]()

Пример 3
Разложим на множители двучлен 8m3 + n3.
Применим формулу (1) и получим ![]()
![]()
Пример 4
Разложим на множители двучлен 64а3 – 27b6.
Представим величины 64а3 и 27b6 в виде кубов величин 4а и 3b2. Используя формулу разности кубов, получаем ![]()
![]()
Пример 5
Докажем, что при всех натуральных n значение выражения ![]() кратно 7.
кратно 7.
Применим формулу (1) и получим
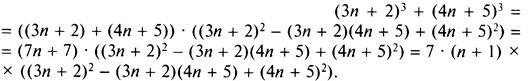
Видно, что данное выражение имеет множитель 7, поэтому оно кратно 7.
Пример 6
Упростим выражение ![]()
![]()
Используя формулы (2) и (1), получим ![]()
![]()
IV. Задания на уроках
№ 905 (а, г, д), 906 (г-е), 907 (в, г), 909 (а, д), 911 (в), 912 (д), 913 (а, б).
V. Контрольные вопросы
— Сформулируйте словами, чему равна сумма кубов, и запишите соответствующую формулу.
— Выведите формулу суммы кубов алгебраическим способом.
— Сформулируйте словами, чему равна разность кубов, и запишите соответствующую формулу.
— Выведите формулу разности кубов алгебраическим способом.
VI. Подведение итогов уроков
Домашнее задание
№ 905 (б, в, е), 906 (а-в), 907 (е), 909 (б, в), 911 (г), 912 (е), 913 (в, г).