Математика - Дидактические материалы 6 класс - 2017 год

Самостоятельные работы

С-1. Масштаб

Вариант I

1. Масштаб карты 1 : 200 000. Расстояние между двумя сёлами на карте 10 см. Чему равно расстояние между этими сёлами на местности?

2. Расстояние между двумя городами 40 км. Чему равно расстояние между этими городами на карте, масштаб которой 1 : 1 000 000?

3. Расстояние между городами А и В равно 150 км. Расстояние между городами А и B на карте равно 3 см. Определите масштаб карты.

4*. Земельный участок на плане имеет вид прямоугольника со сторонами 5 см и 4 см. Определите площадь участка на местности, если масштаб карты равен 1 :500.

Вариант II

1. Масштаб карты 1 : 1 000 000. Расстояние между двумя сёлами на карте 8 см. Чему равно расстояние между этими сёлами на местности?

2. Расстояние между двумя городами 100 км. Чему равно расстояние между этими городами на карте, масштаб которой 1 : 2 000 000?

3. Расстояние между городами А и В равно 140 км. Расстояние между городами А и B на карте равно 7 см. Определите масштаб карты.

4*. Земельный участок на плане имеет вид прямоугольника со сторонами 6 см и 5 см. Определите площадь участка на местности, если масштаб карты равен 1 : 500.

Вариант III

1. Масштаб карты 1 : 250 000. Расстояние между двумя сёлами на карте 16 см. Чему равно расстояние между этими сёлами на местности?

2. Расстояние между двумя городами 24 км. Чему равно расстояние между этими городами на карте, масштаб которой 1 : 400 000?

3. Расстояние между городами А и B равно 200 км. Расстояние между городами А и B на карте равно 8 см. Определите масштаб карты.

4*. Земельный участок на плане имеет вид прямоугольника, площадь которого равна 10 см². Определите площадь участка на местности, если масштаб карты равен 1 : 1000.

Вариант IV

1. Масштаб карты 1 : 125 000. Расстояние между двумя сёлами на карте 12 см. Чему равно расстояние между этими сёлами на местности?

2. Расстояние между двумя городами 25 км. Чему равно расстояние между этими городами на карте, масштаб которой 1 : 500 000?

3. Расстояние между городами А и B равно 360 км. Расстояние между городами А и B на карте равно 9 см. Определите масштаб карты.

4*. Земельный участок на плане имеет вид прямоугольника, площадь которого равна 15 см². Определите площадь участка на местности, если масштаб карты равен 1 : 1000.

С-2. Деление числа в данном отношении

Вариант I

1. Разделите число 125 в отношении:

а) 1 : 4; б) 3 : 2.

2. Начертите отрезок АB, длина которого 14 см. Разделите этот отрезок в отношении 3 : 4.

3. Разделите число 120 на три части так, чтобы первая относилась ко второй как 1 : 2, а вторая — к третьей как 2 : 3.

4*. Мама хочет разделить 22 конфеты между двумя детьми в отношении, обратном отношению их возрастов. Определите, сколько конфет достанется брату, если ему 6 лет, а его сестре 5 лет.

Вариант II

1. Разделите число 140 в отношении:

а) 1 : 6; б) 2 : 5.

2. Начертите отрезок АВ, длина которого 10 см. Разделите этот отрезок в отношении 2 : 3.

3. Разделите число 160 на три части так, чтобы первая относилась ко второй как 1 : 3, а вторая — к третьей как 3 : 4.

4*. Мама хочет разделить 18 конфет между двумя детьми в отношении, обратном отношению их возрастов. Определите, сколько конфет достанется сестре, если ей 5 лет, а её брату 4 года.

Вариант III

1. Разделите число 150 в отношении:

а) 3 : 2; б) 3 : 12.

2. Начертите отрезок MN, длина которого 15 см. Разделите этот отрезок в отношении 3 : 2.

3. Разделите число 170 на три части так, чтобы первая относилась ко второй как 1 : 2, а вторая — к третьей как 3 : 4.

4*. Мама хочет разделить 6 конфет между двумя детьми в отношении, обратном отношению их возрастов. Определите, сколько конфет достанется брату, если ему 6 лет, а его сестре 3 года.

Вариант IV

1. Разделите число 140 в отношении:

а) 2 : 5; б) 2 : 12.

2. Начертите отрезок MN, длина которого 16 см. Разделите этот отрезок в отношении 3 : 5.

3. Разделите число 260 на три части так, чтобы первая относилась ко второй как 2 : 1, а вторая — к третьей как 3 : 4.

4*. Мама хочет разделить 12 конфет между двумя детьми в отношении, обратном отношению их возрастов. Определите, сколько конфет достанется сестре, если ей 6 лет, а её брату 2 года.

С-3 . Пропорции

Вариант I

1. Из чисел 25, 6, 5, 30 составьте пропорцию.

2. Можно ли составить пропорцию из отношений:

а) 8 : 2 и 3 : 12; б) 7 : 5 и 21 : 15?

3. Решите пропорцию:

4*. Решите пропорцию

Вариант II

1. Из чисел 24, 9, 8, 27 составьте пропорцию.

2. Можно ли составить пропорцию из отношений:

а) 15 : 3 и 25 : 5; б) 8 : 3 и 12 : 32?

3. Решите пропорцию:

4*. Решите пропорцию

Вариант III

1. Из чисел 28, 42, 36, 54 составьте пропорцию.

2. Можно ли составить пропорцию из отношений:

а) 24 : 17 и 34 : 48; б) 13 : 12 и 39 : 36?

3. Решите пропорцию:

4*. Решите пропорцию

Вариант IV

1. Из чисел 26, 39, 36, 24 составьте пропорцию.

2. Можно ли составить пропорцию из отношений:

а) 18 : 17 и 54 : 51; б) 15 : 28 и 56 : 30?

3. Решите пропорцию:

4*. Решите пропорцию

С-4. Понятие о проценте

Вариант I

1. Мужчины составляют 60% всех работающих на заводе. Сколько мужчин работает на заводе, если всех работающих 2500 человек?

2. Найдите число, 12% которого равны 48.

3. Сколько процентов числа 50 составляет число 20?

4*. Найдите число, 6% которого равны 16% числа 75.

Вариант II

1. На швейной фабрике работает 2400 человек, 90% их числа составляют женщины. Сколько женщин работает на швейной фабрике?

2. Найдите число, 15% которого равны 45.

3. Сколько процентов числа 25 составляет число 10?

4*. Найдите число, 4% которого равны 75% числа 16.

Вариант III

1. Мужчины составляют 45% всех работников цеха. Сколько женщин работает в цехе, если всех работников 360 человек?

2. Найдите число, 48% которого равны 12.

3. Сколько процентов числа 60 составляет число 84?

4*. Найдите число, 15% которого равны 17% числа 60.

Вариант IV

1. На предприятии работает 450 человек, 54% их числа составляют женщины. Сколько мужчин работает на предприятии?

2. Найдите число, 60% которого равны 15.

3. Сколько процентов числа 25 составляет число 40?

4*. Найдите число, 16% которого равны 15% числа 80.

С-5 . Задачи на проценты

Вариант I

1. Вчера продали 180 кг овощей, а сегодня — на 20% меньше, чем вчера. Сколько килограммов овощей продали за эти два дня?

2. Задумали число, увеличили его на 25% и получили 750. Какое число задумали?

3. На сколько процентов число 120 меньше, чем число 200?

4*. На сколько процентов число 20 больше, чем число 16?

Вариант II

1. Вчера продали 150 кг фруктов, а сегодня — на 30% больше, чем вчера. Сколько килограммов фруктов продано за эти два дня?

2. Задумали число, уменьшили его на 20% и получили 320. Какое число задумали?

3. На сколько процентов число 220 больше, чем число 200?

4*. На сколько процентов число 16 меньше, чем число 20?

Вариант III

1. Туристы проехали на автобусе 220 км, а оставшиеся 45% намеченного маршрута они проехали на электричке. Какова длина намеченного маршрута?

2. Задумали число, увеличили его на 65% и получили 33. Какое число задумали?

3. На сколько процентов число 8 меньше, чем число 10?

4*. На сколько процентов число 15 больше, чем число 12?

Вариант IV

1. Туристы проехали на автобусе 55% намеченного маршрута, а оставшиеся 180 км они проехали на электричке. Какова длина намеченного маршрута?

2. Задумали число, уменьшили его на 75% и получили 80. Какое число задумали?

3. На сколько процентов число 10 больше, чем число 8?

4*. На сколько процентов число 12 меньше, чем число 15?

С-6* . Вероятность события

Вариант I

1. Запишите все трёхзначные числа, в записи которых есть только цифры 0, 5, 7:

а) без повторения цифр;

б) с повторением цифр.

2. Подбросили игральный кубик. Какова вероятность того, что выпадет:

а) 4 очка;

б) нечётное число очков?

3. Какова вероятность того, что при подбрасывании монеты два раза оба раза выпадет орёл?

4*. Случайным образом из натуральных чисел от 22 до 44 выбрали одно число. Какова вероятность того, что оно делится на 9?

Вариант II

1. Запишите все трёхзначные числа, в записи которых есть только цифры 0, 9, 3:

а) без повторения цифр;

б) с повторением цифр.

2. Подбросили игральный кубик. Какова вероятность того, что выпадет:

а) 5 очков;

б) чётное число очков?

3. Какова вероятность того, что при подбрасывании монеты два раза оба раза выпадет решка?

4*. Случайным образом из натуральных чисел от 13 до 35 выбрали одно число. Какова вероятность того, что оно делится на 9?

Вариант III

1. Сколько имеется четырёхзначных чисел, в записи которых есть только цифры 0, 6, 7, 9:

а) без повторения цифр;

б) с повторением цифр?

2. Подбросили игральный кубик. Какова вероятность того, что выпадет:

а) 4 очка или 5 очков;

б) 0 очков?

3. Какова вероятность того, что при подбрасывании монеты два раза сначала выпадет орёл, потом решка?

4*. Случайным образом из натуральных чисел от 14 до 39 выбрали одно число. Какова вероятность того, что оно делится на 2?

Вариант IV

1. Сколько имеется четырёхзначных чисел, в записи которых есть только цифры 0, 4, 6, 8:

а) без повторения цифр;

б) с повторением цифр?

2. Подбросили игральный кубик. Какова вероятность того, что выпадет:

а) 3 очка или 4 очка;

б) 7 очков?

3. Какова вероятность того, что при подбрасывании монеты два раза сначала выпадет решка, потом орёл?

4*. Случайным образом из натуральных чисел от 25 до 55 выбрали одно число. Какова вероятность того, что оно делится на 3?

С-7*. Задачи на вычисление вероятности события

Вариант I

1. В игре “Морской бой” на поле 10 X 10 располагают 1 четырёхпалубный корабль (4 клетки), 2 трёхпалубных корабля (по 3 клетки), 3 двухпалубных корабля (по 2 клетки) и 4 однопалубных корабля (по 1 клетке). Какова вероятность того, что игрок, не видя размещения кораблей на игровом поле и сделав один выстрел (назвав координаты одной клетки), попадёт в четырёхпалубный корабль?

2. В шкафу есть 3 вертикальных ряда по 4 ящика в каждом. В один из ящиков в каждом ряду спрятали по одной монете. Какова вероятность того, что, выдвинув случайным образом по одному ящику в каждом ряду, можно найти монеты в двух первых рядах и не найти в третьем?

3*. Учитель запланировал проверить две домашние работы из пяти на текущей неделе. Эти две работы он выбирает случайным образом и за невыполнение домашней работы ставит в журнал отметку “1”. Определите вероятность события “Вася получит ровно одну “1”, если он не выполнит три домашние работы из этих пяти.

Вариант II

1. В игре “Морской бой” на поле 10 х Ю располагают 1 четырёхпалубный корабль (4 клетки), 2 трёхпалубных корабля (по 3 клетки), 3 двухпалубных корабля (по 2 клетки) и 4 однопалубных корабля (по 1 клетке). Какова вероятность того, что игрок, не видя размещения кораблей на игровом поле и сделав один выстрел (назвав координаты одной клетки), попадёт хотя бы в один однопалубный корабль?

2. В шкафу есть 3 вертикальных ряда по 4 ящика в каждом. В один ящик в каждом ряду спрятали одну монету. Какова вероятность того, что, выдвинув случайным образом по одному ящику в каждом ряду, можно найти монеты в первом ряду и не найти в остальных?

3*. Учитель запланировал проверить две домашние работы из пяти на текущей неделе. Эти две работы он выбирает случайным образом и за невыполнение домашней работы ставит в журнал отметку “1”. Определите вероятность события “Боря получит две “1”, если он не выполнит три домашние работы из этих пяти.

Вариант III

2. В шкафу есть 4 вертикальных ряда по 4 ящика в каждом. В один из ящиков в каждом ряду спрятали по одной монете. Какова вероятность того, что, выдвинув случайным образом по одному ящику в каждом ряду, можно найти монеты в трёх первых рядах и не найти в четвёртом?

3*. Учитель запланировал проверить две домашние работы из шести на текущей неделе. Эти две работы он выбирает случайным образом и за невыполнение домашней работы ставит в журнал отметку “1”. Определите вероятность события “Катя получит одну “1”, если она не выполнит одну домашнюю работу из этих шести.

Вариант IV

1. В игре “Морской бой” на поле 10 х 10 располагают 1 четырёхпалубный корабль (4 клетки), 2 трёхпалубных корабля (по 3 клетки), 3 двухпалубных корабля (по 2 клетки) и 4 однопалубных корабля (по 1 клетке). Какова вероятность того, что игрок, не видя размещения кораблей на игровом поле и сделав один выстрел (назвав координаты одной клетки), попадёт хотя бы в один трёхпалубный корабль?

2. В шкафу есть 4 вертикальных ряда по 4 ящика в каждом. В один из ящиков в каждом ряду спрятали по одной монете. Какова вероятность того, что, выдвинув случайным образом по одному ящику в каждом ряду, можно найти монеты в третьем и четвёртом рядах и не найти в остальных?

3*. Учитель запланировал проверить две домашние работы из шести на текущей неделе. Эти две работы он выбирает случайным образом и за невыполнение домашней работы ставит в журнал отметку “1”. Определите вероятность события “Оля получит хотя бы одну “1”, если она не выполнит две домашние работы из этих шести.

С-8. Модуль целого числа. Сравнение целых чисел

Вариант I

1. Запишите числа, противоположные числам: +5; -2; 0.

2. Определите модули чисел: +8; -6; 0.

3. Упростите записи чисел: -(+5); -(-3); +(-6).

4. Сравните числа:

а) +6 и 0;

б) -8 и 0;

в) -9 и +3;

г) -11 и -7;

д) +20 и +30;

е) -20 и -30.

5*. Сколько целых чисел расположено между числами -14 и +13?

Вариант II

1. Запишите числа, противоположные числам: +7; -4; 0.

2. Определите модули чисел: +5; -8; 0.

3. Упростите записи чисел: +(-7); -(+9); -(-7).

4. Сравните числа:

а) -3 и 0;

б) +8 и 0;

в) -11 и +8;

г) -12 и -9;

д) +30 и +40;

е) -30 и -40.

5*. Сколько целых чисел расположено между числами -16 и +17?

Вариант III

1. Запишите числа, противоположные числам: +15; 0; -12.

2. Определите модули чисел: +13; -60; 0.

3. Упростите записи чисел: -(+20); -(-21); +(-22); +(+23).

4. Сравните числа:

а) +12 и 0;

б) -21 и 0;

в) -10 и +4;

г) -10 и -11;

д) +300 и +200;

е) -300 и -200.

5*. Сколько целых чисел расположено между числами -21 и +22?

Вариант IV

1. Запишите числа, противоположные числам: +12; 0; -16.

2. Определите модули чисел: +11; 0; -34.

3. Упростите записи чисел: +(+10); +(-11); -(-12); -(+13).

4. Сравните числа:

а) +22 и 0;

б) -11 и 0;

в) -16 и +5;

г) -18 и -17;

д) +300 и +400;

е) -300 и -400.

5*. Сколько целых чисел расположено между числами -22 и +23?

С-9. Сложение и вычитание целых чисел

Вариант I

Вычислите (1-5):

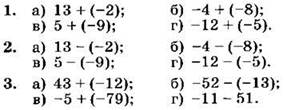
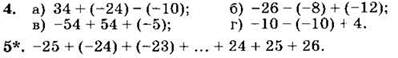
Вариант II

Вычислите (1—5):

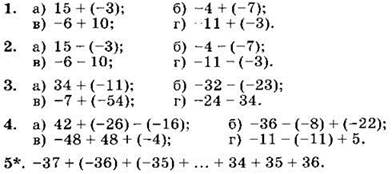
Вариант III

Вычислите (1—5):

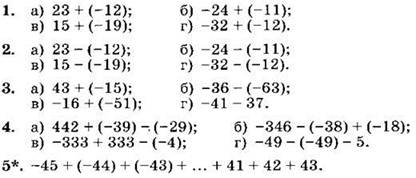
Вариант IV

Вычислите (1—5):

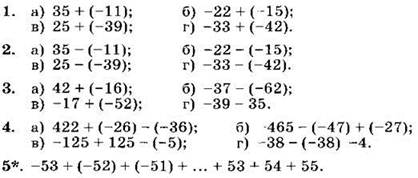
С-10. Умножение и деление целых чисел

Вариант I

Вычислите (1—3):

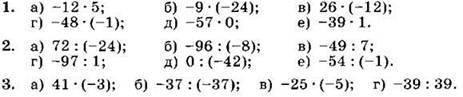
4. Найдите значение выражения

5*. Найдите значение выражения

Вариант II

Вычислите (1—3):

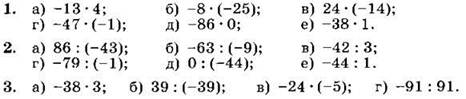
4. Найдите значение выражения

5*. Найдите значение выражения

Вариант III

Вычислите (1—3):

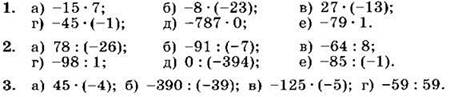
4. Найдите значение выражения

5*. Найдите значение выражения

Вариант IV

Вычислите (1—3):

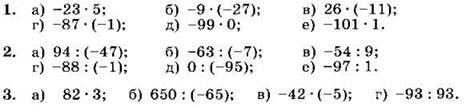
4. Найдите значение выражения

5*. Найдите значение выражения

С-11 . Действия с целыми числами

Вариант I

Найдите значение выражения (1—4):

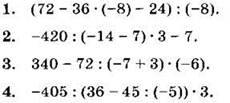
5*. При каком значении а не имеет смысла выражение 200 : ((-55 : 5 + 9) ∙ 24 + а)?

Вариант II

Найдите значение выражения (1—4):

5*. При каком значении а не имеет смысла выражение 300 : ((-66 : 11 + 4) ∙ 25 - а)?

Вариант III

Найдите значение выражения (1—4):

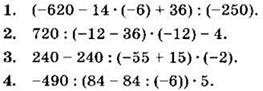
5*. При каком значении а не имеет смысла выражение 400 : ((-88 : 11 + 2) ∙ 36 - а)?

Вариант IV

Найдите значение выражения (1—4):

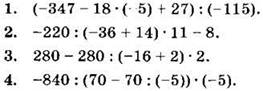
5*. При каком значении а не имеет смысла выражение 500 : ((-77 : 7 + 7) ∙ 23 + а)?

С-12. Представление целых чисел на координатной прямой

Вариант I

1. Запишите координаты точек А, В, С и D, изображённых на рисунке.

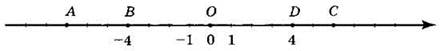
Определите расстояния OD, OB, BD.

2. Изобразите координатную ось, выбрав удобный единичный отрезок, и отметьте на ней точки O(0), М(2), N(-3), K(5) и L(-6). Определите расстояния OL и MN.

3. Различные точки заданы своими координатами: O(0), М(m), N(n). Сравните модули целых чисел m и n, если ОМ > ON.

4*. Определите координату точки М отрезка АВ, если А(-6) и В(4) и AM : МВ = 1 : 4.

Вариант II

1. Запишите координаты точек А, В, С и D, изображённых на рисунке.

Определите расстояния ОС, ОА, АС.

2. Изобразите координатную ось, выбрав удобный единичный отрезок, и отметьте на ней точки O(0), М(3), N(-2), К(6) и L(-7). Определите расстояния ОК и ML.

3. Различные точки заданы своими координатами: O(0), M(m), N(n). Сравните модули целых чисел тип, если ОМ < ON.

4*. Определите координату точки М отрезка АВ, если А(-7) и В(5) и AM : МВ = 1 : 5.

Вариант III

1. Запишите координаты точек А, В, С и D, изображённых на рисунке.

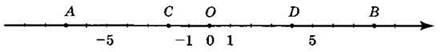
Определите расстояния ОА, OD, AD.

2. Изобразите координатную ось, выбрав удобный единичный отрезок, и отметьте на ней точки O(0), М(4), N(-5), К(1) и L(-8). Определите расстояния OL и МК.

3. Различные точки заданы своими координатами: O(0), М(m), N(n). Определите знак числа m, если ОМ > ON и m < n.

4*. Определите координату точки М отрезка АВ, если А(-8) и B(7) и AM : МB = 2 : 3.

Вариант IV

1. Запишите координаты точек А, В, С и D, изображённых на рисунке.

Определите расстояния ОС, АО, АС.

2. Изобразите координатную ось, выбрав удобный единичный отрезок, и отметьте на ней точки O(0), М(4), N(-3), К(7) и L(-6). Определите расстояния ОК и ML.

3. Различные точки заданы своими координатами: O(0), М(m), N(n). Определите знак числа п, если ОМ < ON и m > n.

4*. Определите координату точки М отрезка АВ, если А(-7) и В(3) и AM : МВ = 3 : 2.

С-13 . Рациональные числа

Вариант I

1. Запишите числа, противоположные числам:

2. Упростите записи чисел:

3. Определите модули чисел:

4. Запишите число в виде дроби:

а) с отрицательным числителем;

б) с отрицательным знаменателем.

5. Сократите дроби

6. Приведите к знаменателю 100 дроби:

7*. Запишите числа: — в виде дробей с положительными знаменателями.

Вариант II

1. Запишите числа, противоположные числам:

2. Упростите записи чисел:

3. Определите модули чисел:

4. Запишите число в виде дроби:

а) с отрицательным знаменателем;

б) с отрицательным числителем.

5. Сократите дроби:

6. Приведите к знаменателю 100 дроби:

7*. Запишите числа: — в виде дробей с положительными знаменателями.

Вариант III

1. Запишите числа, противоположные числам:

2. Упростите записи чисел:

3. Определите модули чисел:

4. Запишите число в виде дроби с отрицательным числителем.

5. Сократите дроби:

6. Приведите к знаменателю 120 дроби:

7*. Запишите числа: — в виде дробей с положительными знаменателями.

Вариант IV

1. Запишите числа, противоположные числам:

2. Упростите записи чисел:

3. Определите модули чисел:

4. Запишите число в виде дроби с отрицательным знаменателем.

5. Сократите дроби:

6. Приведите к знаменателю 150 дроби:

7*. Запишите числа: — в виде дробей с положительными знаменателями.

С-14. Сравнение рациональных чисел

Вариант I

Сравните числа (1—4):

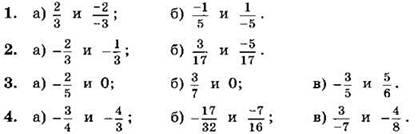
5*. Найдите все несократимые дроби со знаменателем 5, заключённые между числами

Вариант II

Сравните числа (1—4):

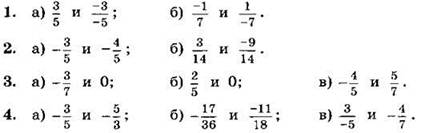
5*. Найдите все несократимые дроби со знаменателем 5, заключённые между числами

Вариант III

Сравните числа (1—4):

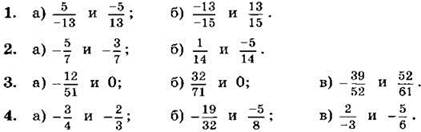
5*. Найдите все несократимые дроби со знаменателем 8, заключённые между числами

Вариант IV

Сравните числа (1—4):

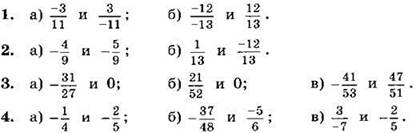
5*. Найдите все несократимые дроби со знаменателем 8, заключённые между числами

С-15 . Сложение рациональных чисел

Вариант I

Выполните сложение (1—2):

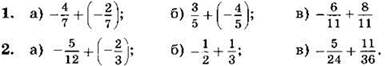
3. Выполните сложение и упростите ответ:

4*. Найдите значение числового выражения

Вариант II

Выполните сложение (1—2):

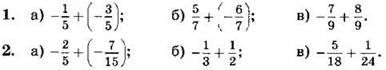
3. Выполните сложение и упростите ответ:

4*. Найдите значение числового выражения

Вариант III

Выполните сложение (1—2):

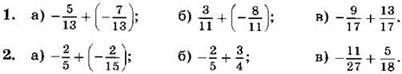
3. Выполните сложение и упростите ответ:

4*. Найдите значение числового выражения

Вариант IV

Выполните сложение (1—2):

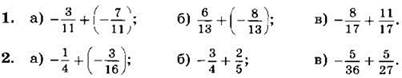
3. Выполните сложение и упростите ответ:

4*. Найдите значение числового выражения

С-16 . Вычитание рациональных чисел

Вариант I

Выполните вычитание (1—2):

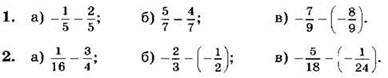
3. Выполните вычитание и упростите ответ:

4*. Найдите значение числового выражения

Вариант II

Выполните вычитание (1—2):

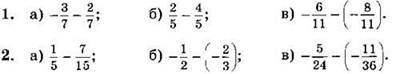
3. Выполните вычитание и упростите ответ:

4*. Найдите значение числового выражения

Вариант III

Выполните вычитание (1—2):

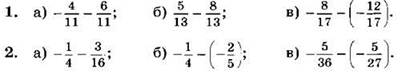
3. Выполните вычитание и упростите ответ:

4*. Найдите значение числового выражения

Вариант IV

Выполните вычитание (1—2):

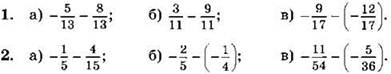
3. Выполните вычитание и упростите ответ:

4*. Найдите значение числового выражения

С-17. Умножение рациональных чисел

Вариант I

1. Выполните умножение:

Выполните умножение и упростите ответ (2—3):

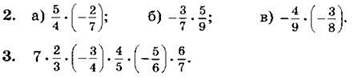
4*. Подберите такую несократимую дробь для которой верно равенство

Вариант II

1. Выполните умножение:

Выполните умножение и упростите ответ (2—3):

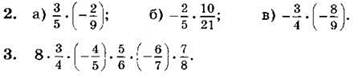
4*. Подберите такую несократимую дробь для которой верно равенство

Вариант III

1. Выполните умножение:

Выполните умножение и упростите ответ (2—3):

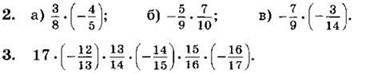
4*. Подберите такую несократимую дробь для которой верно равенство

Вариант IV

1. Выполните умножение:

Выполните умножение и упростите ответ (2—3):

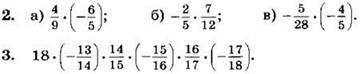
4*. Подберите такую несократимую дробь для которой верно равенство

С-18 . Деление рациональных чисел

Вариант I

1. Выполните деление:

Выполните деление и упростите ответ (2—4):

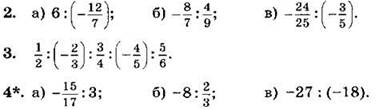
Вариант II

1. Выполните деление:

Выполните деление и упростите ответ (2—4):

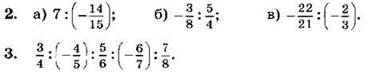
Вариант III

1. Выполните деление:

Выполните деление и упростите ответ (2—4):

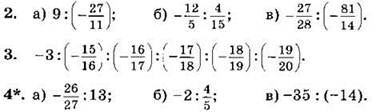
Вариант IV

1. Выполните деление:

Выполните деление и упростите ответ (2—4):

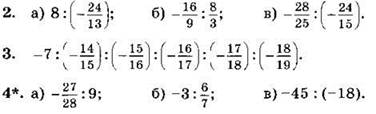
С-19 . Смешанные дроби

Вариант I

1. Запишите в виде смешанной дроби обыкновенную дробь:

2. Запишите в виде обыкновенной дроби смешанную дробь:

3. Вычислите:

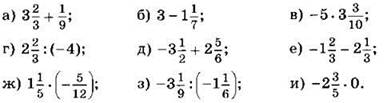
Вычислите, применяя распределительный закон (4—5):

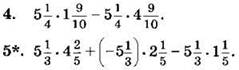
Вариант II

1. Запишите в виде смешанной дроби обыкновенную дробь:

2. Запишите в виде обыкновенной дроби смешанную дробь:

3. Вычислите:

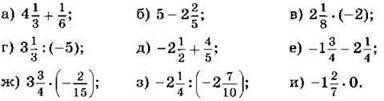
Вычислите, применяя распределительный закон (4—5):

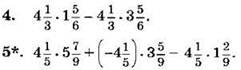
Вариант III

1. Запишите в виде смешанной дроби обыкновенную дробь:

2. Запишите в виде обыкновенной дроби смешанную дробь:

Вычислите:

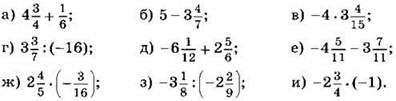
Вычислите, применяя распределительный закон (4—5):

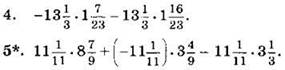
Вариант IV

1. Запишите в виде смешанной дроби обыкновенную дробь:

2. Запишите в виде обыкновенной дроби смешанную дробь:

3. Вычислите:

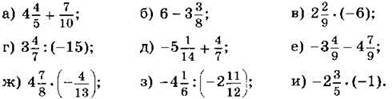
Вычислите, применяя распределительный закон (4—5):

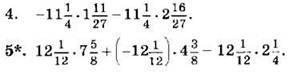
С-20 . Действия с рациональными числами

Вариант I

Найдите значение выражения (1—5):

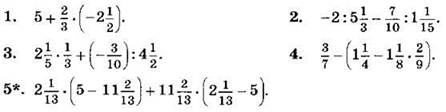
Вариант II

Найдите значение выражения (1—5):

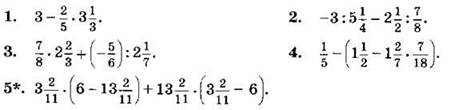
Вариант III

Найдите значение выражения (1—5):

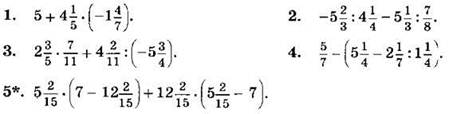
Вариант IV

Найдите значение выражения (1—5):

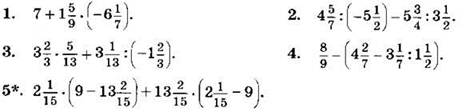
С-21. Представление рациональных чисел на координатной прямой

Вариант I

1. Запишите координаты точек А, В, С и D, изображённых на рисунке.

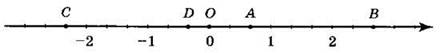
2. Изобразите координатную ось, выбрав удобный единичный отрезок, и отметьте на ней точки O(0), Определите:

а) расстояние МК;

б) координату середины отрезка МК.

3. Вычислите среднее арифметическое чисел: а) 3 и 8; б) 3, 8 и 10.

4. Среднее арифметическое двух рациональных чисел m и n больше нуля. Сравните модули чисел m и n, если известно, что m > 0, n < 0.

5*. Определите координату точки М отрезка АВ, если и AM : МВ = 3 : 4.

Вариант II

1. Запишите координаты точек А, В, С и D, изображённых на рисунке.

2. Изобразите координатную ось, выбрав удобный единичный отрезок, и отметьте на ней точки O(0), Определите:

а) расстояние NL;

б) координату середины отрезка KL.

3. Вычислите среднее арифметическое чисел: а) 5 и 7; б) 5, 7 и 9.

4. Среднее арифметическое двух рациональных чисел m и n меньше нуля. Сравните модули чисел m и n, если известно, что m > 0, n < 0.

5*. Определите координату точки М отрезка АВ, если и AM : МВ = 3 : 4.

Вариант III

1. Запишите координаты точек А, В, С и D, изображённых на рисунке.

2. Изобразите координатную ось, выбрав удобный единичный отрезок, и отметьте на ней точки O(0), Определите:

а) расстояние KL;

б) координату середины отрезка NL.

3. Вычислите среднее арифметическое чисел: а) -7 и 3; б) 6, -1 и 8; в) 5, 6, 7 и 10.

4. Среднее арифметическое двух рациональных чисел m и n больше нуля. Сравните модули чисел m и n, если известно, что m > n.

5*. Определите координату точки М отрезка АВ, если и AM : МВ = 5 : 6.

Вариант IV

1. Запишите координаты точек А, В, С и D, изображённых на рисунке.

2. Изобразите координатную ось, выбрав удобный единичный отрезок, и отметьте на ней точки O(0), Определите:

а) расстояние ML;

б) координату середины отрезка NK.

3. Вычислите среднее арифметическое чисел: а) -5 и 9; б) 7, -2 и 9; в) 4, 5, 8 и 9.

4. Среднее арифметическое двух рациональных чисел m и n меньше нуля. Сравните модули чисел m и n, если известно, что m > n.

5*. Определите координату точки М отрезка АВ, если и AM : МВ = 6 : 5.

С-22. Уравнения

Вариант I

1. Определите, какое из чисел 3, 5, -2 является корнем уравнения х + (8 - 3х) = 12.

Решите уравнение (2—4):

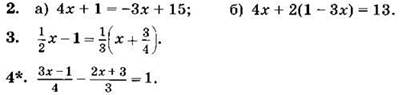
Вариант II

1. Определите, какое из чисел 4, 6, -3 является корнем уравнения х + (7 - 2х) = 10.

Решите уравнение (2—4):

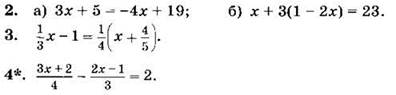
Вариант III

1. Определите, какое из чисел -3, -5, 2 является корнем уравнения 2х + (11 - 4х) = 21.

Решите уравнение (2—4):

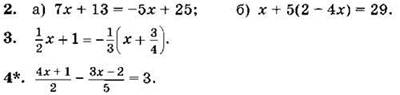
Вариант IV

1. Определите, какое из чисел -3, -4, 4 является корнем уравнения 3х + (13 - 8х) = 33.

Решите уравнение (2—4):

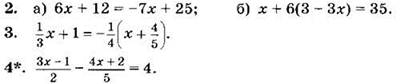
С-23*. Уравнения с модулями

Вариант I

Решите уравнение (1—4):

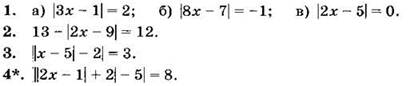
Вариант II

Решите уравнение (1—4):

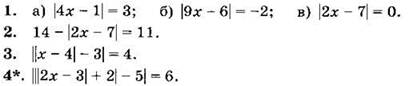
Вариант III

Решите уравнение (1—4):

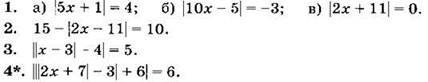
Вариант IV

Решите уравнение (1—4):

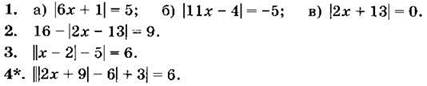
С-24*. Решение задач с помощью уравнений

Вариант I

1. Обозначьте одну неизвестную величину буквой х, выразите через х другую неизвестную величину, составьте уравнение по условию задачи:

а) Одно число в 6 раз больше другого, а их сумма равна 140. Найдите меньшее число.

б) Одно число в 5 раз больше другого, а их разность равна 160. Найдите меньшее число.

в) Брат на 5 лет старше сестры, а сумма их возрастов 23 года. Сколько лет сестре?

Решите задачу с помощью уравнения (2—3):

2. За 4 одинаковых блокнота и 2 одинаковых альбома заплатили 112 р. Один альбом дороже одного блокнота на 8 р. Сколько стоит один блокнот?

3*. В первом классе было 28 учащихся, а во втором — половина числа учащихся первого и третьего классов вместе. Всего в трёх классах было 90 учащихся. Сколько учащихся было во втором классе?

Вариант II

а) Одно число в 5 раз больше другого, а их сумма равна 180. Найдите меньшее число.

б) Одно число в 6 раз больше другого, а их разность равна 120. Найдите меньшее число.

в) У сестры на 20 р. больше, чем у брата, а вместе у них 100 р. Сколько рублей у брата?

Решите задачу с помощью уравнения (2—3):

2. За 4 булочки и 2 ватрушки заплатили 68 р. Одна ватрушка на 4 р. дороже одной булочки. Сколько стоит одна булочка?

3*. В первом классе было 29 учащихся, а во втором — половина числа учащихся первого и третьего классов вместе. Всего в трёх классах было 84 учащихся. Сколько учащихся было во втором классе?

Вариант III

а) Одно число в 7 раз больше другого, а их сумма равна 440. Найдите большее число.

б) Одно число в 8 раз больше другого, а их разность равна 420. Найдите большее число.

в) Сегодня Катя выполнила домашнее задание по математике на 10 мин быстрее, чем вчера, а за эти два дня она потратила на домашние задания по математике 60 мин. Сколько минут Катя выполняла домашнее задание по математике вчера?

Решите задачу с помощью уравнения (2—3):

2. Первую часть пути поезд прошёл за 5 ч, а вторую — за 3 ч. Первую часть пути он шёл с некоторой постоянной скоростью, а вторую часть пути — со скоростью, на 10 км/ч большей. Всего он прошёл 510 км. Чему равна скорость поезда на первом участке пути?

3*. Ученик задумал число, увеличил его в 2 раза, к полученному числу прибавил задуманное, затем полученную сумму уменьшил в 4 раза и получил 27. Какое число он задумал?

Вариант IV

а) Одно число в 8 раз больше другого, а их сумма равна 360. Найдите большее число.

б) Одно число в 7 раз больше другого, а их разность равна 360. Найдите большее число.

в) Сегодня Вася прочитал на 6 страниц больше, чем вчера, а за эти два дня он прочитал 56 страниц. Сколько страниц он прочитал вчера?

Решите задачу с помощью уравнения (2—3):

2. Первую часть пути автомобиль проехал за 4 ч, а вторую — за 3 ч. Первую часть пути он ехал с некоторой постоянной скоростью, а вторую часть пути — со скоростью, на 10 км/ч большей. Всего он проехал 520 км. Чему равна скорость автомобиля на первом участке пути?

3*. Ученик задумал число, увеличил его в 3 раза, к полученному числу прибавил задуманное, затем полученную сумму уменьшил в 3 раза и получил 28. Какое число он задумал?

С-25 . Упрощение выражений

Вариант I

1. Приведите подобные слагаемые:

2. Упростите выражение:

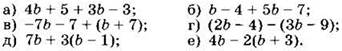
3. Задумали число, прибавили к нему 20, результат умножили на 2 и из полученного числа вычли удвоенное задуманное число. Какое число получили в результате всех вычислений?

4*. Докажите, что значение выражения 7(8х - 1) - 11(х + 13) - 45х - 1 не зависит от х.

Вариант II

1. Приведите подобные слагаемые:

2. Упростите выражение:

3. Задумали число, прибавили к нему 10, результат умножили на 3 и из полученного числа вычли утроенное задуманное число. Какое число получили в результате всех вычислений?

4*. Докажите, что значение выражения 8(7x + 3) - 22(х - 1) - 34х + 9 не зависит от х.

Вариант III

1. Приведите подобные слагаемые:

2. Упростите выражение:

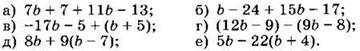
3. Задумали число, прибавили к нему 20, результат умножили на 2 и к тому, что получилось, прибавили 7. Из полученного числа вычли удвоенное задуманное число. Какое число получили в результате всех вычислений?

4*. Докажите, что значение выражения 6(7x + 1) - 33(x + 13) - 9х - 13 не зависит от х.

Вариант IV

1. Приведите подобные слагаемые:

2. Упростите выражение:

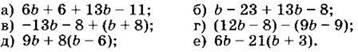
3. Задумали число, прибавили к нему 10, результат умножили на 3 и к тому, что получилось, прибавили 6. Из полученного числа вычли утроенное задуманное число. Какое число получили в результате всех вычислений?

4*. Докажите, что значение выражения 7(6x - 3) - 44(x + 13) + 2х + 15 не зависит от x.

С-26. Десятичные дроби. Сравнение десятичных дробей

Вариант I

1. Запишите десятичную дробь в виде обыкновенной дроби:

а) 0,3; б) 0,24; в) 3,025; г) 4,50.

2. Запишите обыкновенную дробь в виде десятичной дроби:

3. Запишите величину, используя десятичную дробь:

а) 13 р. 45 к.; б) 5 м 2 дм; в) 4 т 50 кг.

4. Сравните десятичные дроби:

а) 3,80 и 3,8;

б) 52,47 и 52,7;

в) 4,003 и 4,03;

г) 3,51 и 4.

5*. Сравните дроби:

Вариант II

1. Запишите десятичную дробь в виде обыкновенной дроби:

а) 0,7; б) 0,25; в) 3,012; г) 3,40.

2. Запишите обыкновенную дробь в виде десятичной дроби:

3. Запишите величину, используя десятичную дробь:

а) 28 р. 12 к.; б) 2 м 5 дм; в) 5 т 40 кг.

4. Сравните десятичные дроби:

а) 8,3 и 8,30;

б) 43,58 и 43,8;

в) 3,04 и 3,004;

г) 5,41 и 6.

5*. Сравните дроби:

Вариант III

1. Запишите десятичную дробь в виде обыкновенной дроби:

а) 0,15; б) 2,08; в) 5,036; г) 6,050.

2. Запишите обыкновенную дробь в виде десятичной дроби:

3. Запишите величину, используя десятичную дробь:

а) 32 р. 5 к.; б) 6 м 3 дм; в) 7 т 5 кг.

4. Сравните десятичные дроби:

а) 5,070 и 5,07;

б) 42,43 и 42,34;

в) 7,006 и 7,06;

г) 7,56 и 8.

5*. Сравните дроби:

Вариант IV

1. Запишите десятичную дробь в виде обыкновенной дроби:

а) 0,45; б) 3,04; в) 4,075; г) 5,050.

2. Запишите обыкновенную дробь в виде десятичной дроби:

3. Запишите величину, используя десятичную дробь:

а) 19 р. 7 к.; б) 3 м 6 дм; в) 5 т 7 кг.

4. Сравните десятичные дроби:

а) 7,050 и 7,05;

б) 43,42 и 43,24;

в) 6,07 и 6,007;

г) 6,51 и 7.

5*. Сравните дроби:

С-27. Сложение и вычитание десятичных дробей

Вариант I

1. Вычислите:

Найдите значение выражения (2—3):

Вариант II

1. Вычислите:

Найдите значение выражения (2—3):

Вариант III

1. Вычислите:

Найдите значение выражения (2—3):

Вариант IV

1. Вычислите:

Найдите значение выражения (2—3):

С-28 . Умножение десятичных дробей

Вариант I

1. Вычислите:

2. Известно, что 123 ∙ 654 = 80 442. Вычислите:

3. Вычислите:

4*. Найдите значение числового выражения

Вариант II

1. Вычислите:

2. Известно, что 321 ∙ 234 = 75 114. Вычислите:

3. Вычислите:

4*. Найдите значение числового выражения

Вариант III

1. Вычислите:

2. Известно, что 234 ∙ 765 = 179 010. Вычислите:

3. Вычислите:

4*. Найдите значение числового выражения

Вариант IV

1. Вычислите:

2. Известно, что 432 ∙ 345 = 149 040. Вычислите:

3. Вычислите:

4*. Найдите значение числового выражения

С-29. Деление десятичных дробей

Вариант I

1. Вычислите:

2. Перенесите запятую в делимом и делителе так, чтобы делитель стал натуральным числом:

3. Вычислите:

4*. Найдите значение выражения

Вариант II

1. Вычислите:

2. Перенесите запятую в делимом и делителе так, чтобы делитель стал натуральным числом:

3. Вычислите:

4*. Найдите значение выражения

Вариант III

1. Вычислите:

2. Перенесите запятую в делимом и делителе так, чтобы делитель стал натуральным числом:

3. Вычислите:

4*. Найдите значение выражения

Вариант IV

1. Вычислите:

2. Перенесите запятую в делимом и делителе так, чтобы делитель стал натуральным числом:

3. Вычислите:

4*. Найдите значение выражения

С-30 . Десятичные дроби и проценты

Вариант I

1. На какую десятичную дробь надо умножить число, чтобы найти:

а) 13% этого числа;

б) 9% этого числа;

в) 120% этого числа?

2. Найдите:

а) 12% числа 450;

б) 8% числа 300;

в) 110% числа 550.

3. Найдите число, если:

а) 24 % этого числа равны 480;

б) 18% этого числа равны 540.

4*. Найдите число, 14% которого равны 17% числа 280.

Вариант II

1. На какую десятичную дробь надо умножить число, чтобы найти:

а) 15% этого числа;

б) 7% этого числа;

в) 130% этого числа?

2. Найдите:

а) 14 % числа 350;

б) 6% числа 700;

в) 120% числа 450.

3. Найдите число, если:

а) 32% этого числа равны 640;

б) 27% этого числа равны 810.

4*. Найдите число, 15% которого равны 16% числа 300.

Вариант III

1. На какую десятичную дробь надо умножить число, чтобы найти:

а) 27% этого числа;

б) 4% этого числа;

в) 140% этого числа?

2. Найдите:

а) 28% числа 650;

б) 3% числа 900;

в) 125% числа 580.

3. Найдите число, если:

а) 34% этого числа равны 17;

б) 36 % этого числа равны 90.

4*. Найдите число, 16% которого равны 15% числа 320.

Вариант IV

1. На какую десятичную дробь надо умножить число, чтобы найти:

а) 29% этого числа;

б) 5% этого числа;

в) 150% этого числа?

2. Найдите:

а) 24% числа 550;

б) 8% числа 700;

в) 135% числа 480.

3. Найдите число, если:

а) 32% этого числа равны 16;

б) 38% этого числа равны 133.

4*. Найдите число, 17% которого равны 14% числа 340.

С-31* . Сложные задачи на проценты

Вариант I

1. Увеличьте число а на 14% этого числа.

2. На какую десятичную дробь надо умножить число а, чтобы увеличить его:

а) на 15%; б) на 20%; в) на 27%?

3. Вкладчик положил в банк 20 000 р. Банк начисляет ежегодно 9% дохода на сумму вклада, находящуюся на счёте вкладчика в начале года. Какая сумма будет на счёте через два года?

4*. Одна акция компании стоила 50 р. Во вторник цена акции повысилась на 10%, а в среду понизилась на 10%. Сколько стала стоить одна акция этой компании после двух изменений цены?

Вариант II

1. Увеличьте число а на 15% этого числа.

2. На какую десятичную дробь надо умножить число а, чтобы увеличить его:

а) на 14%; б) на 25%; в) на 29 %?

3. Вкладчик положил в банк 30 000 р. Банк начисляет ежегодно 8% дохода на сумму вклада, находящуюся на счёте вкладчика в начале года. Какая сумма будет на счёте через два года?

4*. Одна акция компании стоила 100 р. В среду цена акции понизилась на 10%, а в четверг повысилась на 10 %. Сколько стала стоить одна акция этой компании после двух изменений цены?

Вариант III

1. Увеличьте число а на 24% этого числа.

2. На какую десятичную дробь надо умножить число а, чтобы увеличить его:

а) на 21%; б) на 37%; в) на 7,5 %?

3. Вкладчик положил в банк 40 000 р. Банк начисляет ежегодно 11% дохода на сумму вклада, находящуюся на счёте вкладчика в начале года. Какая сумма будет на счёте через два года?

4*. Одна акция компании стоила 150 р. За первую неделю цена акции повысилась на 20 %, а за следующую понизилась на 20 %. Сколько стала стоить одна акция этой компании после двух изменений цены?

Вариант IV

1. Увеличьте число а на 23 % этого числа.

2. На какую десятичную дробь надо умножить число а, чтобы увеличить его:

а) на 22%; б) на 36%; в) на 6,5%?

3. Вкладчик положил в банк 50 000 р. Банк начисляет ежегодно 12% дохода на сумму вклада, находящуюся на счёте вкладчика в начале года. Какая сумма будет на счёте через два года?

4*. Одна акция компании стоила 200 р. За первую неделю цена акции понизилась на 30 %, а за следующую повысилась на 30 %. Сколько стала стоить одна акция этой компании после двух изменений цены?

С-32*. Использование вспомогательных букв при решении задач на проценты

Вариант I

1. Во вторник цена акции повысилась на 30%, в среду она понизилась на 10%. Повысилась или понизилась цена акции за эти два дня и на сколько процентов?

2. У Васи пятёрок на 75% меньше, чем у Коли. На сколько процентов у Коли пятёрок больше, чем у Васи?

3*. Первое число на 40% больше, чем второе, и на 60% меньше, чем третье. На сколько процентов третье число больше, чем второе?

Вариант II

1. Во вторник цена акции повысилась на 10%, в среду она понизилась на 30%. Повысилась или понизилась цена акции за эти два дня и на сколько процентов?

2. У Маши пятёрок на 150% больше, чем у Вали. На сколько процентов у Вали пятёрок меньше, чем у Маши?

3*. Первое число на 40% меньше, чем второе, и на 25% больше, чем третье. На сколько процентов третье число меньше, чем второе?

Вариант III

1. Во вторник цена акции повысилась на 20%, в среду она понизилась на 40%. Повысилась или понизилась цена акции за эти два дня и на сколько процентов?

2. Первое число на 20% меньше, чем второе. На сколько процентов второе число больше, чем первое?

3*. На помидоры мама потратила денег на 25 % меньше, чем на огурцы, и на 200% больше, чем на картофель. На сколько процентов меньше она потратила денег на картофель, чем на огурцы?

Вариант IV

1. Во вторник цена акции повысилась на 40%, в среду она понизилась на 20%. Повысилась или понизилась цена акции за эти два дня и на сколько процентов?

2. Первое число на 25% больше, чем второе. На сколько процентов второе число меньше, чем первое?

3*. На груши папа потратил денег на 50% меньше, чем на сливы, и на 50% больше, чем на яблоки. На сколько процентов больше он потратил денег на сливы, чем на яблоки?

С-33* . Практические задачи на проценты

Вариант I

1. Яблоки при сушке теряют 75% своей массы.

а) Сколько килограммов сушёных яблок получится из 50 кг свежих?

б) Сколько килограммов свежих яблок надо взять, чтобы получить 2,5 кг сушёных?

2. Яблоки содержат 78% воды. При сушке они теряют 75% своей массы. Сколько процентов воды содержат сушёные яблоки?

3*. Яблоки содержат 78% воды. Их немного подсушили, и теперь они содержат 45% воды. Сколько процентов своей массы яблоки потеряли при сушке?

Вариант II

1. Груши при сушке теряют 80% своей массы.

а) Сколько килограммов сушёных груш получится из 45 кг свежих?

б) Сколько килограммов свежих груш надо взять, чтобы получить 3,2 кг сушёных?

2. Груши содержат 83% воды. При сушке они теряют 80% своей массы. Сколько процентов воды содержат сушёные груши?

3*. Груши содержат 83% воды. Их немного подсушили, и теперь они содержат 75% воды. Сколько процентов своей массы груши потеряли при сушке?

Вариант III

1. Сливы при сушке теряют 76% своей массы.

а) Сколько килограммов сушёных слив получится из 60 кг свежих?

б) Сколько килограммов свежих слив надо взять, чтобы получить 28,8 кг сушёных?

2. Сливы содержат 79% воды. При сушке они теряют 76% своей массы. Сколько процентов воды содержат сушёные сливы?

3*. Сливы содержат 79% воды. Их немного подсушили, и теперь они содержат 70% воды. Сколько процентов своей массы сливы потеряли при сушке?

Вариант IV

1. Абрикосы при сушке теряют 65 % своей массы.

а) Сколько килограммов сушёных абрикосов получится из 44 кг свежих?

б) Сколько килограммов свежих абрикосов надо взять, чтобы получить 17,5 кг сушёных?

2. Абрикосы содержат 72% воды. При сушке они теряют 65% своей массы. Сколько процентов воды содержат сушёные абрикосы?

3*. Абрикосы содержат 72% воды. Их немного подсушили, и теперь они содержат 60% воды. Сколько процентов своей массы абрикосы потеряли при сушке?

С-34. Десятичные дроби произвольного знака

Вариант I

Найдите значение выражения (1—5):

Вариант II

Найдите значение выражения (1—5):

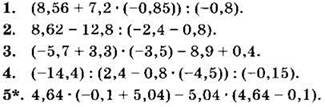
Вариант III

Найдите значение выражения (1—5):

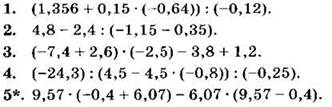
Вариант IV

Найдите значение выражения (1—5):

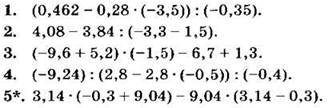
С-35. Совместные действия с обыкновенными и десятичными дробями произвольного знака

Вариант I

Вычислите (1—2):

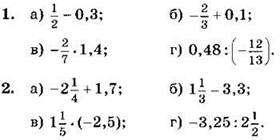
Найдите значение выражения (3—4):

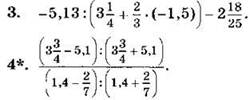
Вариант II

Вычислите (1—2):

Найдите значение выражения (3—4):

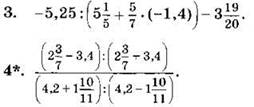
Вариант III

Вычислите (1—2):

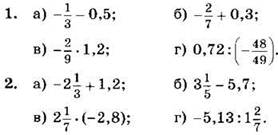
Найдите значение выражения (3—4):

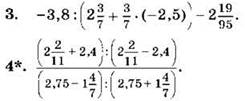
Вариант IV

Вычислите (1—2):

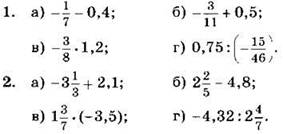
Найдите значение выражения (3—4):

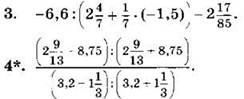
С-36. Приближения десятичных дробей

Вариант I

1. Укажите приближение десятичной дроби 13,529 с недостатком с точностью: а) до одной единицы; б) до одной десятой; в) до одной сотой.

2. Укажите приближение десятичной дроби 13,529 с избытком с точностью: а) до одной единицы; б) до одной десятой; в) до одной сотой.

3. Округлите десятичную дробь 13,529: а) до единиц; б) до десятых; в) до сотых.

4. Округлите десятичную дробь: а) 143,95 до единиц; б) 19,328 до десятых; в) 1,928 до сотых.

5*. Округлите десятичную дробь а = 9382,7461:

а) до единиц;

б) до десятых;

в) до сотых;

г) до тысячных;

д) до десятков;

е) до сотен;

ж) до тысяч.

Вариант II

1. Укажите приближение десятичной дроби 26,294 с недостатком с точностью: а) до одной единицы; б) до одной десятой; в) до одной сотой.

2. Укажите приближение десятичной дроби 26,294 с избытком с точностью: а) до одной единицы; б) до одной десятой; в) до одной сотой.

3. Округлите десятичную дробь 26,294: а) до единиц; б) до десятых; в) до сотых.

4. Округлите десятичную дробь: а) 254,82 до единиц; б) 18,237 до десятых; в) 3,546 до сотых.

5*. Округлите десятичную дробь а = 3829,4617:

а) до единиц;

б) до десятых;

в) до сотых;

г) до тысячных;

д) до десятков;

е) до сотен;

ж) до тысяч.

Вариант III

1. Укажите приближение десятичной дроби 51,738 с недостатком с точностью: а) до одной единицы; б) до одной десятой; в) до одной сотой.

2. Укажите приближение десятичной дроби 51,738 с избытком с точностью: а) до одной единицы; б) до одной десятой; в) до одной сотой.

3. Округлите десятичную дробь 51,738: а) до десятков; б) до единиц; в) до десятых; г) до сотых.

4. Округлите десятичную дробь: а) 149,81 до единиц; б) 24,137 до десятых; в) 11,835 до сотых.

5*. Округлите десятичную дробь а = 8293,6174:

а) до единиц;

б) до десятых;

в) до сотых;

г) до тысячных;

д) до десятков;

е) до сотен;

ж) до тысяч.

Вариант IV

1. Укажите приближение десятичной дроби 25,384 с недостатком с точностью: а) до одной единицы; б) до одной десятой; в) до одной сотой.

2. Укажите приближение десятичной дроби 25,384 с избытком с точностью: а) до одной единицы; б) до одной десятой; в) до одной сотой.

3. Округлите десятичную дробь 25,384: а) до десятков; б) до единиц; в) до десятых; г) до сотых.

4. Округлите десятичную дробь: а) 239,52 до единиц; б) 34,346 до десятых; в) 22,829 до сотых.

5*. Округлите десятичную дробь а = 2938,1746:

а) до единиц;

б) до десятых;

в) до сотых;

г) до тысячных;

д) до десятков;

е) до сотен;

ж) до тысяч.

С-37. Приближённые вычисления

Вариант I

1. Округлив числа а и Ъ с точностью до 0,01, вычислите приближённо сумму а + b и разность а - b:

а) а = 4,8394, b = 1,783;

б) а = 45,394, b = 23,728.

2. Округлите числа а и b с точностью до двух значащих цифр, вычислите приближённо произведение а ∙ b и частное а : b. Результат округлите с точностью до двух значащих цифр:

а) а = 25,19, b = 4,354;

б) а = 53,74, b = 6,637.

3*. Стороны прямоугольника измерили приближённо: а ≈ 12,7 м, b ≈ 4,88 м. Вычислите приближённо:

а) периметр прямоугольника с точностью до десятых долей метра;

б) площадь прямоугольника с точностью до трёх значащих цифр.

Вариант II

1. Округлив числа а и 6 с точностью до 0,01, вычислите приближённо сумму а + b и разность а - b:

а) а = 5,9283, b = 2,694;

б) а = 36,483, b = 44,937.

а) а = 32,27, b = 4,263;

б) а = 46,62, b = 5,729.

3*. Стороны прямоугольника измерили приближённо: а ≈ 13,2 м, b ≈ 4,09 м. Вычислите приближённо:

а) периметр прямоугольника с точностью до десятых долей метра;

б) площадь прямоугольника с точностью до трёх значащих цифр.

Вариант III

1. Округлив числа а и b с точностью до 0,01, вычислите приближённо сумму а + b и разность а - b:

а) а = 5,9082, b = 3,691;

б) а = 38,083, b = 21,906.

2. Округлите числа а и b с точностью до трёх значащих цифр, вычислите приближённо произведение а ∙ b и частное а : b. Результат округлите с точностью до трёх значащих цифр:

а) а = 63,49, b = 6,452;

б) а = 73,519, b = 8,2059.

3*. Стороны прямоугольника измерили приближённо: а ≈ 14,7 м, b ≈ 3,74 м. Вычислите приближённо:

а) периметр прямоугольника с точностью до десятых долей метра;

б) площадь прямоугольника с точностью до трёх значащих цифр.

Вариант IV

1. Округлив числа а и b с точностью до 0,01, вычислите приближённо сумму а + b и разность а - b:

а) а = 2,9362, b = 2,791;

б) а = 39,283, b = 14,809.

а) а = 75,38, b = 8,532;

б) а = 93,428, b = 9,8091.

3*. Стороны прямоугольника измерили приближённо: а ≈ 14,8 м, b ≈ 4,12 м. Вычислите приближённо:

а) периметр прямоугольника с точностью до десятых долей метра;

б) площадь прямоугольника с точностью до трёх значащих цифр.

С-38*. Периодические десятичные дроби

Вариант I

1. Запишите обыкновенную дробь: в виде конечной десятичной дроби или бесконечной периодической десятичной дроби.

2. Покажите, как можно записать в виде обыкновенной дроби периодическую десятичную дробь:

а) 0,(7); б) 0,(15); в) 0,3(4).

3. Покажите, что периодическая дробь 2,1(9) равна конечной десятичной дроби.

4*. Найдите значение выражения

Вариант II

2. Покажите, как можно записать в виде обыкновенной дроби периодическую десятичную дробь:

а) 0,(5); б) 0,(17); в) 0,4(6).

3. Покажите, что периодическая дробь 1,2(9) равна конечной десятичной дроби.

4*. Найдите значение выражения

Вариант III

2. Покажите, как можно записать в виде обыкновенной дроби периодическую десятичную дробь:

а) 0,(97); б) 0,(157); в) 0,3(97).

3. Покажите, что периодическая дробь 5,4(9) равна конечной десятичной дроби.

4*. Найдите значение выражения

Вариант IV

2. Покажите, как можно записать в виде обыкновенной дроби периодическую десятичную дробь:

а) 0,(43); б) 0,(345); в) 0,12(4).

3. Покажите, что периодическая дробь 4,5(9) равна конечной десятичной дроби.

4*. Найдите значение выражения

С-39. Длина окружности и площадь круга

Вариант I

1. Вычислите приближённо длину окружности, если:

а) её радиус равен 5 см; б) её диаметр равен 6 м.

2. Вычислите приближённо площадь круга, если его радиус равен 7 см.

3*. Из справочника выписали приближение числа π ≈ 3,14159265. Сколько первых цифр числа π надо взять для приближённого вычисления:

а) длины окружности, если её радиус приближённо равен 2,56 см;

б) площади круга, если его радиус приближённо равен 1,6 м?

Вычислите приближённо длину окружности и площадь круга.

Вариант II

1. Вычислите приближённо длину окружности, если:

а) её радиус равен 7 см; б) её диаметр равен 8 м.

2. Вычислите приближённо площадь круга, если его радиус равен 8 см.

а) длины окружности, если её радиус приближённо равен 3,24 см;

б) площади круга, если его радиус приближённо равен 1,5 м?

Вычислите приближённо длину окружности и площадь круга.

Вариант III

1. Вычислите приближённо длину окружности, если:

а) её радиус равен 9 см; б) её диаметр равен 10 м.

2. Вычислите приближённо площадь круга, если его радиус равен 11см.

а) длины окружности, если её радиус приближённо равен 4,56 см;

б) площади круга, если его радиус приближённо равен 1,8 м?

Вычислите приближённо длину окружности и площадь круга.

Вариант IV

1. Вычислите приближённо длину окружности, если:

а) её радиус равен 11 см; б) её диаметр равен 12 м.

2. Вычислите приближённо площадь круга, если его радиус равен 9 см.

а) длины окружности, если её радиус приближённо равен 4,65 см;

б) площади круга, если его радиус приближённо равен 1,9 м?

Вычислите приближённо длину окружности и площадь круга.