Поурочные разработки по Математике 5 класс к УМК Н.Я. Виленкина
Окружность и круг - ОБЫКНОВЕННЫЕ ДРОБИ - ДРОБНЫЕ ЧИСЛА
Планируемые предметные результаты: уметь читать, записывать и объяснять значение обыкновенной дроби; узнавать правильные и неправильные дроби, уметь соотносить их с единицей; знать названия чисел при записи обыкновенной дроби, понимать значение дробной черты в записи дроби; выполнять сравнение дробей, выделять целую часть числа и переводить смешанное число в неправильную дробь; выполнять сложение и вычитание дробей с одинаковыми знаменателями.
Планируемые метапредметные результаты: анализировать и осмысливать текст задачи, извлекать из текста необходимую информацию, моделировать с помощью схем, рисунков, реальных предметов, строить логическую цепочку, оценивать полученный результат, осуществлять самоконтроль; доказывать и опровергать утверждения с помощью контрпримеров, классифицировать; исследовать задачи на вычисление площадей и объемов, составлять аналогичные; уметь сравнивать, выделять общее и особенное, делать выводы.
Планируемые личностные результаты: формирование представлений о математике как о части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества; развитие логического и критического мышления, умения работать в группе, команде, уважение мнения товарищей; формирование интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта.
Урок 76. Окружность и круг
Основная дидактическая цель урока: познакомить учащихся с окружностью и кругом; учить строить окружность с помощью циркуля.
Ход урока
I. Организационный момент
II. Устный счет. Определение темы урока
(На доске прикреплены карточки чистой стороной к учащимся. На карточках записаны буквы, которые складываются в название темы урока. Карточки открывают в любом порядке. За правильный ответ учитель открывает одну карточку до тех пор, пока учащиеся не смогут прочитать тему урока.)
![]()
1. Найдите произведение наибольшего и наименьшего двузначных чисел. (990.)
2. Какое из тел имеет больший объем: прямоугольный параллелепипед с измерениями 2 см, 3 см, 4 см или куб с ребром 3 см? (Куб, 24 < 27.)
3. Сколько квадратных метров в одном гектаре? (10 000 м2.)
4. Длина одного отрезка 1 дм 2 см, а длина второго отрезка 6 мм. Во сколько раз первый отрезок длиннее второго? (В 20 раз.)
5. 5! — это сколько? (120.)
6. Сколько кубических сантиметров в одном кубическом метре? (1 000 000 см3.)
7. Найдите произведение чисел 24 и 11. (264.)
8. 3100 : 100?
9. Как называется равенство, содержащее букву? (Уравнение.)
10. Длина прямоугольника 6 см, ширина в 2 раза меньше. Найдите площадь прямоугольника.
— Кто знает, что такое окружность?
— С помощью какого инструмента можно построить окружность?
III. Работа по теме урока
1. С. 133—134 (работа по статье учебника).
— Прочитайте статью учебника и приготовьтесь отвечать на вопросы.
2. Работа в тетради.
Поставьте в тетради точку О, отступив вниз от предыдущей записи 8 клеточек. Возьмите в раствор циркуля отрезок 3 см. Поставьте иголочку в точку О и постройте окружность.
— Как называется точка O?
Окружность — это линия, которая делит плоскость на две части.
— Покажите часть плоскости, которая находится внутри окружности.
— Как она называется?
— Укажите на окружности две любые точки. Соедините их. Какая фигура получилась? (Отрезок.)
— Этот отрезок называется хордой.
— Попробуйте дать определение, что такое хорда.
— Соедините любую точку окружности с центром. Как называется этот отрезок?
— Дайте определение радиуса.
— Сколько радиусов можно провести в одной окружности?
— Начертите еще три.
— Измерьте все радиусы. Что заметили?
— Сделайте вывод.
— Начертите хорду, которая проходит через центр. Как называется эта хорда?
— Измерьте диаметр. Что заметили?
(В ходе беседы выполняются записи в тетради.)
Точка О — центр окружности.
Круг — часть плоскости, ограниченная окружностью.
Хорда — отрезок, соединяющий две любые точки окружности.
Радиус — отрезок, соединяющий центр окружности с любой ее точкой.
Все радиусы одной окружности равны.
Диаметр — отрезок, проходящий через центр и соединяющий две точки окружности.
Диаметр окружности в два раза больше ее радиуса.
3. С. 134, № 850 (письменно).
Лежат на окружности точки: D, В.
Лежат внутри круга точки: А, О, Е.
Не лежат на окружности точки: С, F, Е, А, О.
Лежат вне круга точки: F, С.
4. С. 134, № 852.
5. С. 134, № 853.
IV. Повторение изученного материала
С. 135, № 857 (устно).
— Прочитайте задачу.
— Как называется прибор, который показывает скорость?
— Рассмотрите спидометр.
— С какой максимальной скоростью может двигаться автомобиль?
— Посмотрите, чему равна цена одного деления.
— Как вы это узнали?
— С какой скоростью сейчас движется автомобиль?
— Ответьте на первый вопрос.
— Ответьте на второй вопрос.
— Какой ответ вы дали бы на третий вопрос?
V. Работа над задачей
1. С. 136, № 867.
— Что нужно вычислить для того, чтобы узнать, сколько потребуется краски?
— Что будем узнавать для того, чтобы ответить на второй вопрос задачи?
— Что сказано про расход краски?
— Как вы думаете, в каких единицах удобнее производить вычисления?
— Составьте план решения задачи.
— Решите задачу.
80 см = 8 дм
90 см = 9 дм
70 см = 7 дм
1) S = 8 ∙ 9 ∙ 2 + 9 ∙ 7 + 7 ∙ 8 ∙ 2 = 144 + 63 + 112 = 319 (дм2).
2) 319 ∙ 2 = 638 (дм2) — площадь под покраску.
3) 638 ∙ 2 = 1276 (г) = 1 кг 276 г — столько краски потребуется.
4) V = 8 ∙ 9 ∙ 7 = 504 (дм3) = 504 л.
2. С. 137, № 870.
— Что означает выражение “весы находятся в равновесии”?
— Что сказано про пустую банку?
— Каким способом будем решать задачу?
— Что обозначим через х?
Пусть масса пустой банки будет х.
Тогда масса варенья будет 4х.
Масса банки с вареньем равна х + 4х.
А по условию масса банки с вареньем 1 кг (1000 г).
Значит, можем составить уравнение:
х + 4х = 1000
5х = 1000
х = 1000 : 5
х = 200 (г) — масса пустой банки.
200 ∙ 4 = 800 (г) — масса варенья.
— Как иначе можно узнать массу варенья?
VI. Повторение изученного материала
С. 137, № 872 (работа в паре).
Проверка
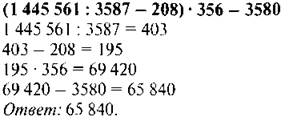
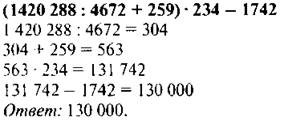
VII. Рефлексия
— Что нового узнали сегодня на уроке?
— Расскажите, что вы запомнили.
Домашнее задание
С. 137, № 874, 875,878 (а, б).