Урок-игра Лабиринт - ПОВТОРЕНИЕ. РЕШЕНИЕ ЗАДАЧ

Основная дидактическая цель урока: развивать логическое мышление, смекалку, сообразительность; воспитывать интерес к предмету.

Ход урока

I. Организационный момент

В каждом из четырех углов класса стоит по одному столу, составленных из двух парт. Это точки лабиринта.

Каждая точка имеет свое название: “Вычислительная”, “Комбинаторика”, “Кроссворд”, “Логика”. В каждой точке лабиринта приготовлено задание дня каждой из команд. (Задание для команд одинаковое.) Каждая команда находится в своей точке лабиринта и выполняет задание. По команде капитаны передают выполненное задание учителю-ведущему. По часовой стрелке команды переходят к другим точкам и выполняют задание там. Пока команды работают на точке, учитель успевает проверить и оценить выполненное командой задание. Так игра проходит до тех пор, пока каждая команда не окажется в той точке, где начинала игру. Время игры распределяется так.

Начало, организация игры — 5 мин.

Игра — по 8 мин в каждой из четырех точек.

Подведение итогов игры — 5 мин.

II. Проведение игры

Право выбора точки лабиринта предоставляется команде, которая быстро даст ответ на вопрос задачи.

В классе четыре точки лабиринта. У нас 4 команды. Сколько различных способов распределения команд по точкам существует? (4! = 24.)

1. Задания в точке “Вычислительная”.

Оценка: команде присуждается 1 балл за каждый правильный ответ.

Условие: найдите значения выражений, используя только устные приемы вычислений. Записать можно только ответ.

234 + 119 + 66 =

45 ∙ 11 =

567 - 299 =

Найдите 25% от 8412.

Найдите 10% от 5710.

35 ∙ 99 =

857 + 198 =

1616 : 16 =

34 ∙ 0,01 =

1,23 : 0,1 =

786 - (470 + 286) =

285 + (319 + 15) =

2. Задания в точке “Комбинаторика”.

Оценка: команде присуждается один балл за каждую верно решенную задачу.

1) На огороде вскопали 4 грядки. На одной надо посадить укроп, на другой — щавель. Сколькими способами это можно сделать? (12.)

2) Сколько существует трехзначных чисел, в записи которых нет нуля? (729.)

3) В классе 10 девочек и 15 мальчиков. Сколько вариантов выбора пары, в которой один мальчик и одна девочка? (150.)

4) В соревнованиях по хоккею участвуют 6 команд. Сколькими способами эти команды могут разыграть между собой золотые и серебряные медали? (30.)

5) Оле надо купить транспортир и треугольник. В магазине 4 вида транспортиров и 5 видов треугольников. Сколькими способами Оля может сделать покупку? (20.)

6) Сколько существует вариантов вывести друг за другом на арену цирка льва, тигра, пуму и медведя? (4! = 24.)

3. Задание в точке “Кроссворд”.

Решив кроссворд, вы прочитаете по вертикали имя великого греческого ученого.

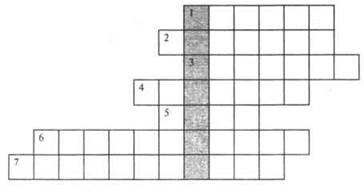
По горизонтали:

1) Угол, равный 90°. (Прямой.)

2) Самая большая хорда. (Диаметр.)

3) Правило, записанное с помощью букв. (Формула.)

4) Прямоугольник, у которого все стороны равны. (Квадрат.)

5) Геометрическая фигура, образованная двумя лучами, исходящими из одной точки. (Угол.)

6) Инструмент для измерения величины углов. (Транспортир.)

7) Луч, который делит угол пополам. (Биссектриса.)

Ответ: Пифагор.

4. Задание в точке “Логическая”.

Оценка: 5 баллов за правильно решенную задачу.

Коля, Боря, Вова и Юра заняли первые четыре места в соревновании. На вопрос, кто какое место занял, ребята ответили:

— Коля — ни первое, ни четвертое.

— Боря занял второе место.

— Вова не был последним из четырех.

Кто какое место занял?

Ответ: первое место занял Вова, второе — Боря, третье — Коля, четвертое — Юра.

III. Рефлексия

— Какое задание показалось трудным?