Угол. Прямой и развернутый угол. Чертежный треугольник - Урок 2 - ИНСТРУМЕНТЫ ДЛЯ ВЫЧИСЛЕНИЙ И ИЗМЕРЕНИЙ - ДРОБНЫЕ ЧИСЛА

Основная дидактическая цель урока: дать понятия “тупой угол”, “острый угол”; учить читать, записывать и находить углы; продолжить работу над текстовыми задачами.

Ход урока

I. Организационный момент

II. Устный счет

1. C. 247, № 1624.

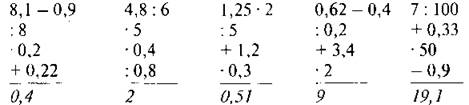
2. На доске (слайде):

Найдите: 8% от 400; 30% от 20; 10% от 46; 25% от 28; 20% от 5. 3.

3. Прочитайте все углы, которые видите.

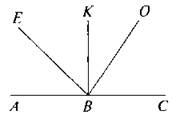
— Есть ли среди углов развернутый? Назовите.

— Есть ли среди углов прямой? Назовите.

III. Определение темы урока

— Попробуйте определить тему урока.

IV. Работа по теме урока

1. Работа по чертежу на с. 377.

— Какой луч проходит внутри ∠KBC?

— На сколько углов этот луч делит прямой угол?

— Сравните величину каждого из этих углов с прямым.

— Все углы, которые меньше прямого, называются острыми.

— Давайте запишем все острые углы, которые есть на чертеже. (∠ABE; ∠EBK; ∠KBO; ∠OBC.)

— Назовите углы на чертеже, которые больше прямого.

— Все углы, которые больше прямого, но меньше развернутого, называются тупыми.

— Запишите все тупые углы, которые вы видите на чертеже. (∠ABO; ∠EBC.)

2. С. 246, № 1616 (работа в паре).

3. С. 246, № 1617.

— Сравните первую пару углов. (∠AOB = ∠BOC.)

— Объясните свое решение.

— Что можно сказать про эти углы? (Они острые.)

— Сравните следующие пары углов. Объясните свое решение.

∠BOC < ∠COD;

∠AOC > ∠AOВ;

∠AOC > ∠COD.

— Назовите все острые углы на рисунке.

— Назовите все тупые углы на рисунке.

4. С. 246, № 1618.

5. С. 246, № 1619 (устно).

V. Повторение изученного материала. Решение задач

1. С. 248, № 1633.

— Что входит в состав бронзы?

— Сколько олова в сплаве?

— Сколько меди в сплаве?

— Что нужно узнать в задаче?

— Что для этого нужно знать?

— Можем ли узнать массу всего сплава?

— Какой вид задачи теперь получился?

— Решите задачу.

1) 6 + 34 = 40 (кг) — масса всего сплава.

2) 34 : 40 = 0,85

3) 0,85 = 85% — столько меди в сплаве.

2. С. 248, № 1634 (работа в паре).

Проверка

Пусть высота башен Московского Кремля будет х.

Тогда высота Александрийского маяка будет 1,7х.

Высота Московского университета будет 1,7х + 119.

Узнаем, на сколько башни Московского Кремля ниже Александрийского маяка: 1,7х — х.

А по условию эта разность равна 49 м.

Значит, можем составить уравнение:

1,7х — x = 49

0,7х = 49

x = 49 : 0,7

x = 70 (м) — высота башен Московского Кремля.

1,7x = 70 ∙ 1,7 = 119 (м) — высота Александрийского маяка.

119 + 119 = 238 (м) — высота Московского университета.

VI. Самостоятельная работа

С. 248, № 1635.

4,5% от 168 (7,56.)

147,6% от 2500 (3690.)

28,3% от 569,8 (161,2534.)

0,09% от 456 800 (411,12.)

VII. Рефлексия

— Что нового узнали сегодня на уроке?

Домашнее задание

С. 248, № 1641; с. 249, № 1643.